TriangularDistribution
TriangularDistribution[{min,max}]
represents a symmetric triangular statistical distribution giving values between min and max.
represents a symmetric triangular statistical distribution giving values between 0 and 1.
TriangularDistribution[{min,max},c]
represents a triangular distribution with mode at c.
Details
- The mean of a pair of uniformly distributed random variables follows a symmetric triangular distribution. »
- TriangularDistribution allows min, max, and c to be any real numbers such that min<c<max.
- TriangularDistribution allows min, max, and c to be quantities of the same unit dimensions. »
- TriangularDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- TriangularDistribution[{min,max},c] represents a continuous statistical distribution supported over the interval min≤x≤max and parametrized by three real numbers min, max, and c (where min<c<max) that specify the lower endpoint of its support, the upper endpoint of its support, and the
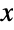 -coordinate of its mode, respectively. In general, the PDF of a triangular distribution is triangular (piecewise linear, concave down, and unimodal) with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of min, max, and c. The one-parameter form TriangularDistribution[{min,max}] is equivalent to TriangularDistribution[{min,max},c] for
-coordinate of its mode, respectively. In general, the PDF of a triangular distribution is triangular (piecewise linear, concave down, and unimodal) with a single "peak" (i.e. a global maximum), though its overall shape (its height, its spread, and the horizontal location of its maximum) is determined by the values of min, max, and c. The one-parameter form TriangularDistribution[{min,max}] is equivalent to TriangularDistribution[{min,max},c] for 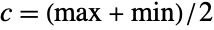 , while the zero-parameter form TriangularDistribution[] is equivalent to TriangularDistribution[{0,1},1/2]. Triangular distributions that are symmetric are sometimes referred to as tine distributions.
, while the zero-parameter form TriangularDistribution[] is equivalent to TriangularDistribution[{0,1},1/2]. Triangular distributions that are symmetric are sometimes referred to as tine distributions. - The triangular distribution dates back to the eighteenth century and the work of English academic Thomas Simpson, though its first modern treatment came in the mid-1930s. Historically, the distribution was used as a tool to model probabilistic quantities related to or stemming from variates modeled by other distributions (e.g. the triangular distribution is the distribution modeling the mean of two uniform random variates), though recently the triangular distribution has been used for modeling in a variety of fields. For example, the triangular distribution is at the center of a wide variety of literature dealing with project evaluation and review techniques. The distribution is also a popular tool in Monte Carlo simulation and has been used to model phenomena in areas such as discrete system simulation, uncertainty and machine learning, finance, and supply chain management.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a triangular distribution. Distributed[x,TriangularDistribution[{min,max},c]], written more concisely as xTriangularDistribution[{min,max},c], can be used to assert that a random variable x is distributed according to a triangular distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for triangular distributions may be given using PDF[TriangularDistribution[{min,max},c],x] and CDF[TriangularDistribution[{min,max},c],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a triangular distribution, EstimatedDistribution to estimate a parametric triangular distribution from given data, and FindDistributionParameters to fit data to a triangular distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic triangular distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic triangular distribution.
- TransformedDistribution can be used to represent a transformed triangular distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a triangular distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving triangular distributions.
- TriangularDistribution is related to a number of other distributions. The mean of two uniform variables follows TriangularDistribution so that the distributions UniformSumDistribution[2,{min,max}] and TriangularDistribution[{min,max}] have proportional characteristic functions (CharacteristicFunction). TriangularDistribution is generalized by BatesDistribution, in the sense that the characteristic function of TriangularDistribution[] is precisely that of BatesDistribution[2], and is also closely related to UniformDistribution, VonMisesDistribution, LogisticDistribution, WeibullDistribution, LaplaceDistribution, and ChiSquareDistribution.
Examples
open allclose allBasic Examples (4)
Scope (8)
Generate a sample of random numbers from a triangular distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness varies with the shape parameter c:
Skewness is 0 in the symmetric case:
Different moments with closed forms as functions of parameters:
Moment has closed form:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
An executive is given an account of historical seasonal demands for a product in millions of units. The minimum, maximum, and most likely demands are 1, 1.4, and 1.25, respectively. Find the expected demand and its standard deviation using TriangularDistribution:
The momentum of a secondary particle from a synchrotron beam is modeled by TriangularDistribution:
The distribution is symmetric and attains maximum at ![]() :
:
Properties & Relations (6)
Triangular distribution is closed under translation and scaling by a positive factor:
Relationships to other distributions:
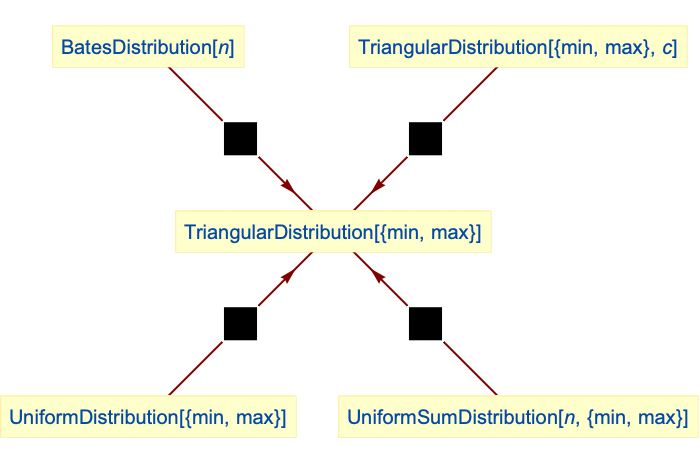
The mean of two uniform variables follows TriangularDistribution:
Triangular distribution is a special case of BatesDistribution:
ArcSinDistribution is a transformation of TriangularDistribution:
The default position for c is in the middle of the support interval:
Possible Issues (2)
TriangularDistribution is not defined when min or max is not real:
TriangularDistribution is not defined when c is not between min and max:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Text
Wolfram Research (2007), TriangularDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangularDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "TriangularDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/TriangularDistribution.html.
APA
Wolfram Language. (2007). TriangularDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangularDistribution.html