BatesDistribution
represents the distribution of a mean of n random variables uniformly distributed from 0 to 1.
BatesDistribution[n,{min,max}]
represents the distribution of a mean of n random variables uniformly distributed from min to max.
Details
- The probability density for value
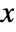in a uniform sum distribution is proportional to 
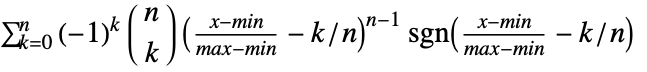for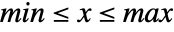 
and zero otherwise. - BatesDistribution[n,{min,max}] is equivalent to TransformedDistribution[(x1+⋯+xn)/n,…] with each xi from UniformDistribution[{min,max}].
- BatesDistribution allows n to be any positive integer and min and max to be any real numbers with min<max.
- BatesDistribution allows min and max to be any quantities with the same unit dimensions and n to be a dimensionless quantity. »
- BatesDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BatesDistribution[n,{min,max}] represents a statistical distribution defined over the interval from min to max and parametrized by a positive integer n. The overall shape of the probability density function (PDF) of a Bates distribution varies significantly depending on n and can be uniform, triangular, or unimodal for
, 
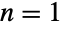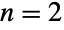, and 
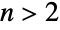, respectively. The one-argument form BatesDistribution[n] is equivalent to BatesDistribution[n,{0,1}] and is sometimes called the standardized Bates distribution. - Mathematically, the Bates distribution BatesDistribution[n] is defined to be the mean of n statistically independent uniformly-distributed random variables
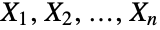, i.e. XBatesDistribution[n] is equivalent to saying that 
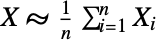, where XiUniformDistribution[] for all 
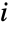. The two-argument form BatesDistribution[n,{min,max}] has the same meaning with the exception that 
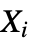UniformDistribution[{min,max}]. One important application of the Bates distribution is in computing, where the standardized Bates distribution with 
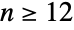was used historically to generate standard normal variables. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Bates distribution. Distributed[x,BatesDistribution[n,{min,max}]], written more concisely as xBatesDistribution[n,{min,max}], can be used to assert that a random variable x is distributed according to a Bates distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BatesDistribution[n,{min,max}],x] and CDF[BatesDistribution[n,{min,max}],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Bates distribution, EstimatedDistribution to estimate a Bates parametric distribution from given data, and FindDistributionParameters to fit data to a Bates distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Bates distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Bates distribution.
- TransformedDistribution can be used to represent a transformed Bates distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Bates distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Bates distributions.
- BatesDistribution is closely related to a number of other distributions. For example, the PDF of a Bates distribution is precisely UniformDistribution and TriangularDistribution for
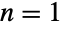and 
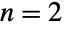, respectively, and appears visually similar to the PDF of NormalDistribution for larger values of 
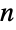. BatesDistribution is also closely related to UniformSumDistribution, which represents the sum of statistically independent, uniformly distributed random variables (rather than their mean).
Examples
open allclose allScope (8)
Generate a sample of pseudorandom numbers from a Bates distribution:
Compare the sampled data histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the data histogram with the PDF of the estimated distribution:
Kurtosis does not depend on the domain:
In the limit, kurtosis is the same as kurtosis of NormalDistribution:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
The mean of a uniform distribution follows a Bates distribution:
A device has 3 lifetime phases: A, B, and C. The time in hours spent in each phase follows uniform distribution over 
, and after phase C, failure occurs. Find the distribution of the average time spent in the same phase:
Find the mean average time spent in the same phase:
Find the probability that on average the device will stay in the same stage for more than 4 hours:
Simulate the average time spent in the same phase for 30 such devices:
Properties & Relations (5)
Bates distribution is closed under translation and scaling:
Scaling with a negative factor:
The default domain is interval 
:
Relationships to other distributions:
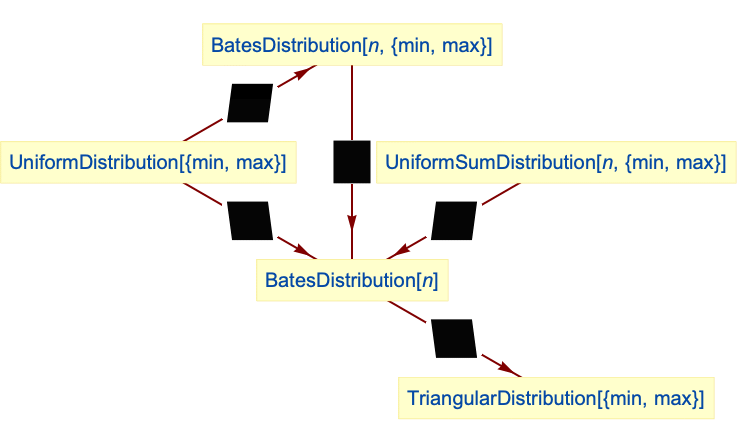
The distribution of the mean of n uniformly distributed variables follows the Bates distribution:
The triangular distribution is a special case of the Bates distribution:
Text
Wolfram Research (2010), BatesDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BatesDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BatesDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BatesDistribution.html.
APA
Wolfram Language. (2010). BatesDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BatesDistribution.html