GumbelDistribution[α,β]
represents a Gumbel distribution with location parameter α and scale parameter β.
represents a Gumbel distribution with location parameter 0 and scale parameter 1.


GumbelDistribution
GumbelDistribution[α,β]
represents a Gumbel distribution with location parameter α and scale parameter β.
represents a Gumbel distribution with location parameter 0 and scale parameter 1.
Details
- The Gumbel distribution gives the asymptotic distribution of the minimum value in a sample from a distribution such as the normal distribution.
- The asymptotic distribution of the maximum value, also sometimes called a Gumbel distribution, is implemented in the Wolfram Language as ExtremeValueDistribution. »
- The probability density for value
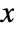 in a Gumbel distribution is proportional to
in a Gumbel distribution is proportional to 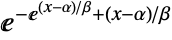 . »
. » - GumbelDistribution allows α to be any real number and β to be any positive real number.
- GumbelDistribution allows α and β to be any quantities of the same unit dimensions. »
- GumbelDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- GumbelDistribution[α,β] represents a continuous statistical distribution defined over the real numbers and parametrized by a real number α (the "location parameter") and a positive real number β (the "scale parameter"). The probability density function (PDF) of a Gumbel distribution is unimodal, and the parameter α controls the horizontal location, while β determines the overall height and steepness of the PDF. In addition, the tails of the PDF are "thin", in the sense that the PDF decreases exponentially for large values of
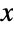 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Gumbel distribution is sometimes referred to as a type-1 extreme value distribution (not to be confused with "the" extreme value distribution, implemented in the Wolfram Language as ExtremeValueDistribution), the doubly exponential distribution (not to be confused with LaplaceDistribution, which may also be called doubly exponential), or the log-Weibull distribution (cf. WeibullDistribution).
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) The Gumbel distribution is sometimes referred to as a type-1 extreme value distribution (not to be confused with "the" extreme value distribution, implemented in the Wolfram Language as ExtremeValueDistribution), the doubly exponential distribution (not to be confused with LaplaceDistribution, which may also be called doubly exponential), or the log-Weibull distribution (cf. WeibullDistribution). - GumbelDistribution is one of four distributions (along with FrechetDistribution, ExtremeValueDistribution, and WeibullDistribution) classified under the general heading "extreme value distributions", all of which are used as tools for quantifying "extreme" or "rare" events (i.e. those that are "extremely unlikely", having datasets consisting of variates with extreme deviations from the median). The Gumbel distribution is named for German mathematician Emil Julius Gumbel, who studied it in the late 1930s as a limit distribution for the smallest order statistic (i.e. as a potential asymptotic distribution for the minimum value of a sample with some other underlying distribution). Since its inception, the Gumbel distribution has been used to model a number of real-world phenomena, including human lifetimes, radioactive emissions, evolutionary genetic mutations, flood and seismic analyses, droughts, and catastrophic insurance losses. The Gumbel distribution has also been used in number theory to approximate the number of terms in a partition of an integer (see IntegerPartitions), as well as the sizes of record prime gaps.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Gumbel distribution. Distributed[x,GumbelDistribution[α,β]], written more concisely as xGumbelDistribution[α,β], can be used to assert that a random variable x is distributed according to a Gumbel distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[GumbelDistribution[α,β],x] and CDF[GumbelDistribution[α,β],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Gumbel distribution, EstimatedDistribution to estimate a Gumbel parametric distribution from given data, and FindDistributionParameters to fit data to a Gumbel distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Gumbel distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Gumbel distribution.
- TransformedDistribution can be used to represent a transformed Gumbel distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Gumbel distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Gumbel distributions.
- The Gumbel distribution is related to several other distributions. As mentioned previously, GumbelDistribution shares qualitative relationships with ExtremeValueDistribution, FrechetDistribution, and WeibullDistribution. These relationships can be quantified by noting that the PDF of GumbelDistribution[α,β] is precisely the same as that of both TransformedDistribution[-u,u ExtremeValueDistribution[-α,β]] and TransformedDistribution[β α Log[u/β]+α,u WeibullDistribution[α,β]], and that FrechetDistribution is a transformed WeibullDistribution. GumbelDistribution is related to MinStableDistribution and MaxStableDistribution, in the sense that the PDF of GumbelDistribution[α,β], MinStableDistribution[α,β,0], and TransformedDistribution[-u,u MaxStableDistribution[-α,β,0]] are all the same. GumbelDistribution is also related to LogisticDistribution, ExpGammaDistribution, GompertzMakehamDistribution, and ExponentialDistribution.
Examples
open all close allBasic Examples (4)
Scope (7)
Generate a sample of pseudorandom numbers from a Gumbel distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness and kurtosis are constant:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (2)
The lifetime of a device has a Gumbel distribution. Find the reliability of the device:
The hazard function is exponentially increasing in time:
Find the reliability of two such devices in series:
Find the reliability of two such devices in parallel:
Compare the reliability of both systems for ![]() and
and ![]() :
:
The magnitude of the annual maximum earthquake can be modeled using GumbelDistribution. Consider earthquakes in the United States in the past 200 years:
Create a sample eliminating the missing data:
Fit a Gumbel distribution to the data:
Compare the histogram of the sample with the PDF of the estimated distribution:
Find the probability of the annual maximum earthquake having a magnitude of at least 6:
Find the average magnitude of the annual maximum earthquake:
Simulate the magnitudes of the annual maximum earthquake for 30 years:
Properties & Relations (15)
Gumbel distribution is closed under translation and scaling by a positive factor:
With arbitrary parameter values:
Skewness is the negative of the skewness of ExtremeValueDistribution:
ExtremeValueDistribution is skewed to the right, while GumbelDistribution is skewed to the left:
Kurtosis is the same as for ExtremeValueDistribution:
The family of GumbelDistribution is closed under a minimum:
The CDF of GumbelDistribution solves the minimum stability postulate equation:
Relationships to other distributions:
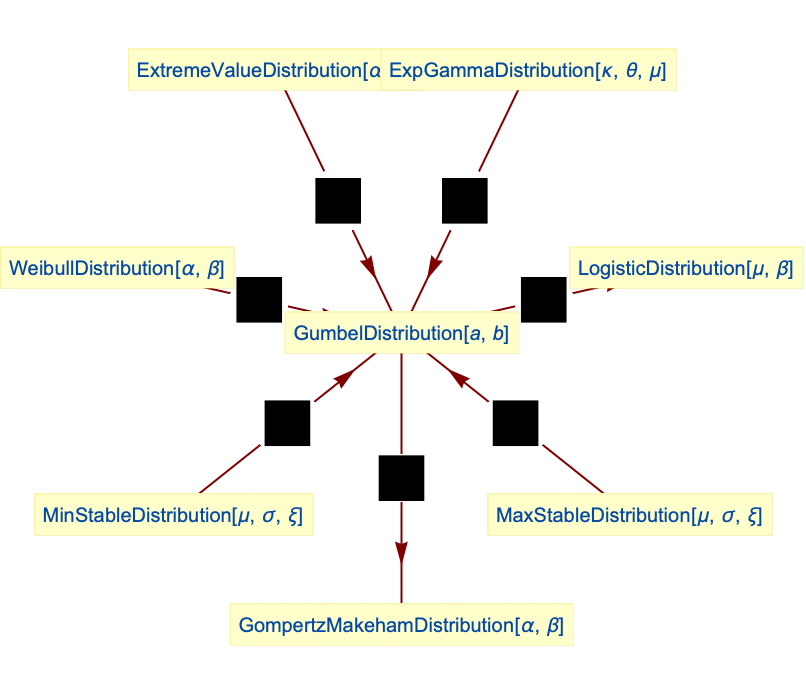
GumbelDistribution is the negative of ExtremeValueDistribution:
GumbelDistribution is a transformation of WeibullDistribution:
A truncated Gumbel distribution is a GompertzMakehamDistribution:
GumbelDistribution is a special case of MinStableDistribution:
GumbelDistribution is a transformation of MaxStableDistribution:
The difference of two variates from GumbelDistribution follows the same distribution as the difference of two variates from ExtremeValueDistribution, which is LogisticDistribution:
The sum of a Gumbel distribution and ExtremeValueDistribution follows LogisticDistribution:
GumbelDistribution is a special case of ExpGammaDistribution:
ParameterMixtureDistribution of ExtremeValueDistribution with Gumbel distribution follows LogisticDistribution:
Possible Issues (3)
The distribution of minimum values is given by GumbelDistribution:
The distribution of maximum values is given by ExtremeValueDistribution:
GumbelDistribution is not defined when α is not a real number:
GumbelDistribution is not defined when β is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
Tech Notes
Text
Wolfram Research (2007), GumbelDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/GumbelDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "GumbelDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GumbelDistribution.html.
APA
Wolfram Language. (2007). GumbelDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GumbelDistribution.html
BibTeX
@misc{reference.wolfram_2025_gumbeldistribution, author="Wolfram Research", title="{GumbelDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GumbelDistribution.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_gumbeldistribution, organization={Wolfram Research}, title={GumbelDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/GumbelDistribution.html}, note=[Accessed: 24-February-2026]}