LQGRegulator

LQGRegulator[sspec,cvs,wts]

gives the optimal output feedback controller for the stochastic system specification sspec with noise covariance matrices cvs that minimizes a cost function with weights wts.

LQGRegulator[…,"prop"]

gives the value of the property "prop".

Details and Options

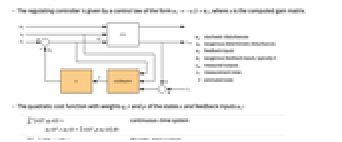
  • LQGRegulator is also known as linear quadratic Gaussian controller or stochastic linear controller.
  • LQGRegulator is used to compute a regulating controller or tracking controller for a system with disturbances and measurement noise modeled as zero-mean, Gaussian, white noise processes.
  • LQGRegulator works by minimizing a quadratic cost function of the states and feedback inputs, and the sum of the variances of the error between the actual and estimated states.
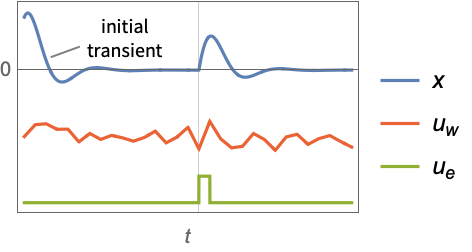
  • A regulating controller aims to maintain the system at an equilibrium state despite disturbances uw and ue interfering with it. Typical examples include maintaining an inverted pendulum in its upright position or maintaining an aircraft in level flight.
  • The regulating controller is given by a control law of the form 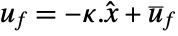, where 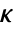is the computed gain matrix.
  • The quadratic cost function with weights q, r and p of the states x and feedback inputs uf:
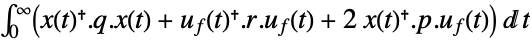
  • continuous-time system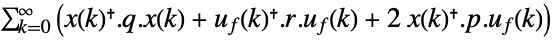
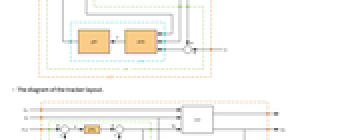
    discrete-time system
  • A tracking controller aims to track a reference signal despite disturbances uw and ue interfering with it. Typical examples include a cruise control system for a car or path tracking for a robot.
  • The tracking controller is given by a control law of the form 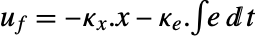, where 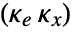is the computed gain matrix for the augmented system, which includes the system sys as well as the dynamics for .
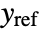  • The quadratic cost function with weights q, r and p of the augmented states 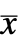and feedback inputs uf:
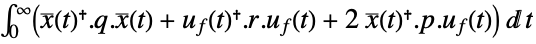
  • continuous-time system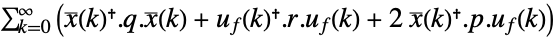
    discrete-time system
  • The number of states of the augmented system is given by 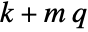, where 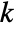is given by SystemsModelOrder of sys, 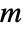the order of yref and 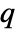the number of signals yref.
  • The choice of weighting matrices results in a tradeoff between performance and control effort, and a good design is arrived at iteratively. Their starting values can be diagonal matrices with entries TemplateBox[{{1, /, z}, i, 2}, Subsuperscript], where zi is the maximum admissible absolute value of the corresponding xi or ui.
  • The weights wts can have the following forms:
  • {q,r}cost function with no cross-coupling
    {q,r,p}cost function with cross-coupling matrix p
  • The measurements ym are modeled as 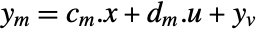, where 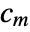and 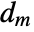are the submatrices of 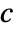and 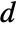associated with 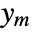, and 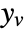is the noise.
  • The stochastic inputs uw and the measurement noise yv are considered to be zero-mean, white and Gaussian:
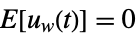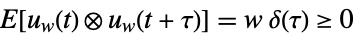
  • , process noise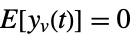
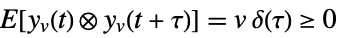
    , measurement noise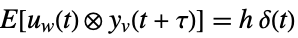
    cross covariance
  • The covariance matrices cvs can have the following forms:
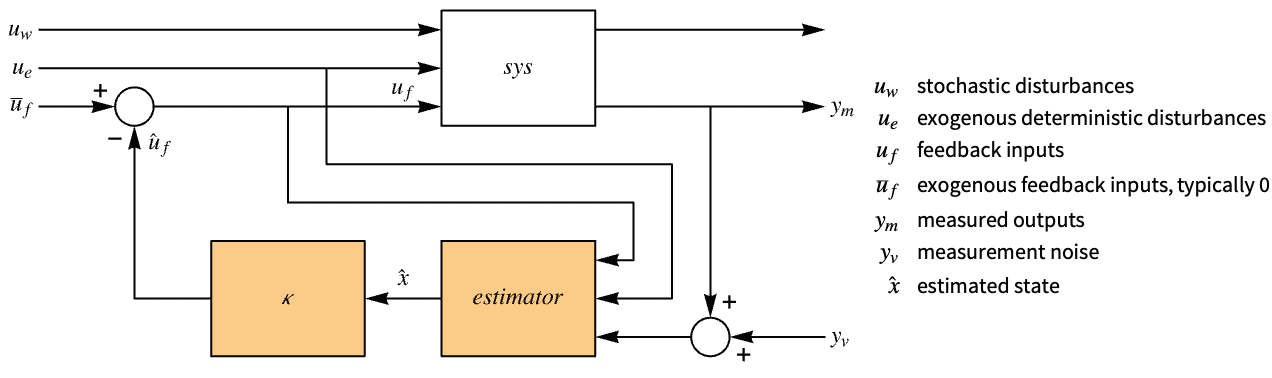
  • {w,v}covariance matrices and zero cross covariance
    {w,v,h}covariance and cross covariance matrices
  • The system specification sspec is the system sys together with the uf, ue, yt and yref specifications.
  • The system specification sspec can have the following forms:
  • StateSpaceModel[…]linear control input and linear state
    AffineStateSpaceModel[…]linear control input and nonlinear state
    NonlinearStateSpaceModel[…]nonlinear control input and nonlinear state
    SystemModel[…]general system model
    <|…|>detailed system specification given as an Association
  • The detailed system specification can have the following keys:
  • "InputModel"sysany one of the models
    "FeedbackInputs"Allthe feedback inputs uf
    "ExogenousInputs"Nonethe exogenous inputs ue
    "MeasuredOutputs"Allthe measured outputs ym
    "TrackedOutputs"Nonetracked outputs yt
    "TrackedSignal"Automaticthe dynamics of yref
  • The inputs and outputs can have the following forms:
  • {num1,…,numn}numbered inputs or outputs numi used by StateSpaceModel, AffineStateSpaceModel and NonlinearStateSpaceModel
    {name1,…,namen}named inputs or outputs namei used by SystemModel
    Alluses all inputs or outputs
    Noneuses none of the inputs or outputs
  • LQGRegulator[…,"Data"] returns a SystemsModelControllerData object cd that can be used to extract additional properties using the form cd["prop"].
  • LQGRegulator[…,"prop"] can be used to directly get the value of cd["prop"].
  • Possible values for properties "prop" include:
  • "ClosedLoopPoles"poles of "ClosedLoopSystem"
    "ClosedLoopSystem"system csys
    {"ClosedLoopSystem",cspec}detailed control over the form of the closed-loop system
    "ControllerModel"model cm
    "Design"type of controller design
    "EstimatorGains"gain matrix ℓ
    "EstimatorGainsDesignModel"model used for the estimator gains design
    "EstimatorRegulatorFeedbackModel"model with ue, ym as input and 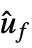as output
    "EstimatorRegulatorModel"model erm with uf, ue, ym as input and 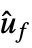as output
    "ExogenousInputs"deterministic and non-feedback inputs ue of sys
    "FeedbackGains"gain matrix κ or its equivalent
    "FeedbackGainsDesignModel"model used for the feedback gains design
    "FeedbackGainsModel"model gm or {gm1,gm2}
    "FeedbackInputs"inputs uf of sys used for feedback
    "InputModel"input model sys
    "InputCount"number of inputs u of sys
    "MeasuredOutputs"measured outputs ym of sys
    "OpenLoopPoles"poles of the Taylor linearized sys
    "OutputCount"number of outputs y of sys
    "SamplingPeriod"sampling period of sys
    "StateEstimatorModel"model sem
    "StateOutputEstimatorModel"model soem
    "StateCount"number of states x of sys
    "TrackedOutputs"outputs yt of sys that are tracked
  • Possible keys for cspec include:
  • "InputModel"input model in csys
    "Merge"whether to merge csys
    "ModelName"name of csys
  • The diagram of the regulator layout.
  • The diagram of the tracker layout.

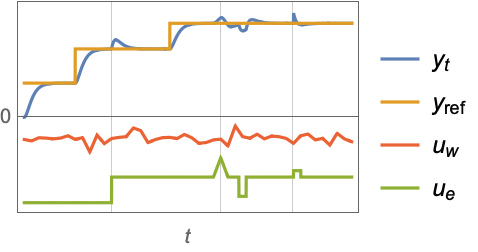
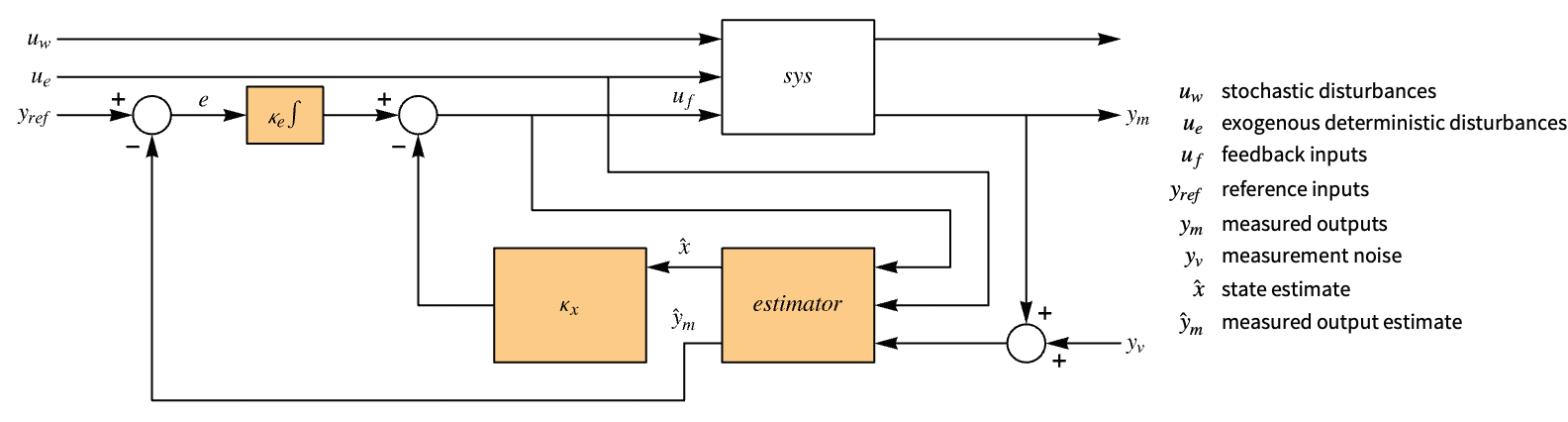
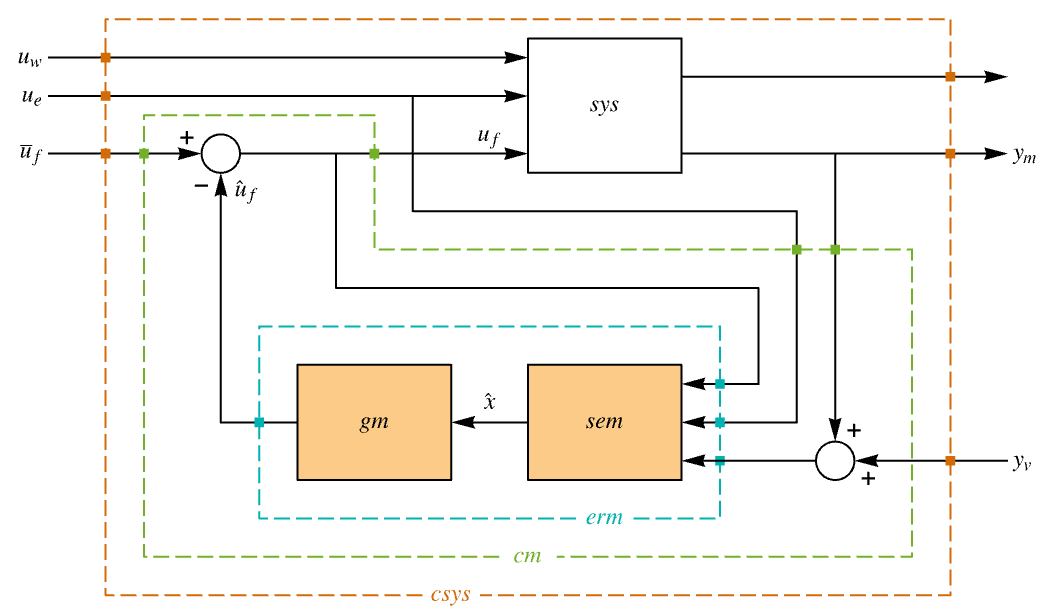
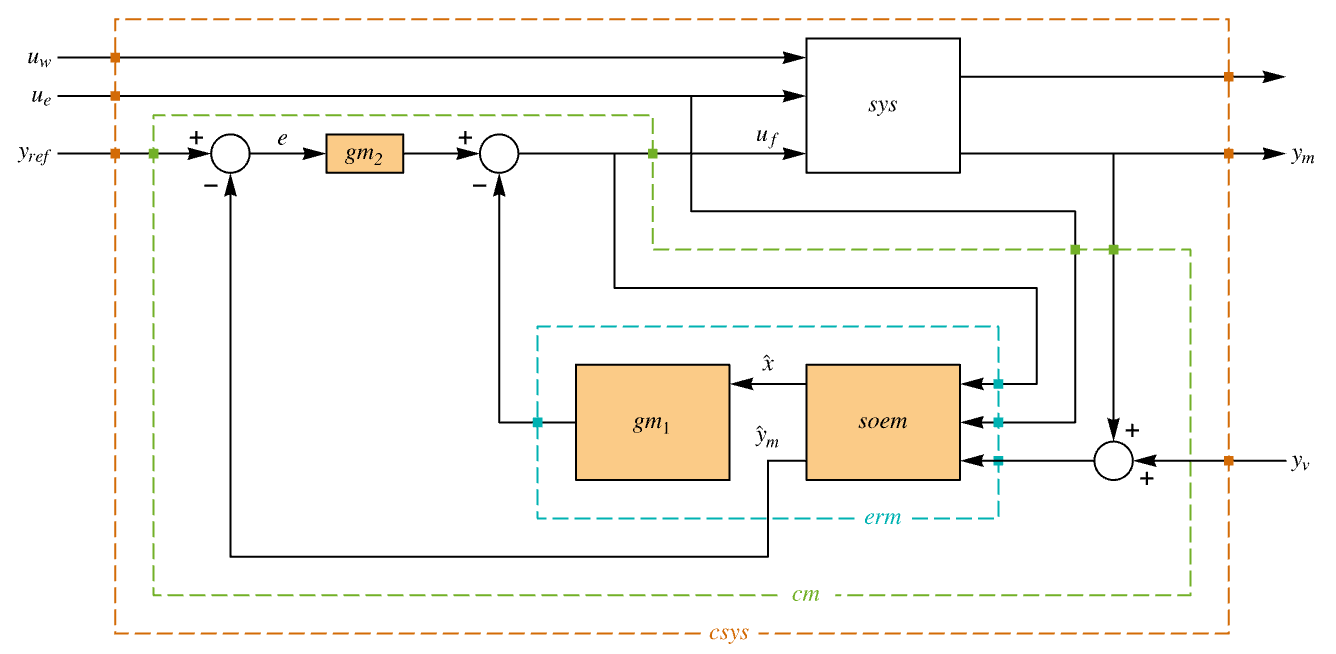
Examples

open allclose all

Basic Examples  (4)

A system specification sspec of a system with feedback input uf and process noise input uw:

A set of noise covariance matrices cvs and regulator weights wts:

The LQG controller:

A nonlinear system:

A set of noise covariance matrices cvs and regulator weights wts:

The LQG controller:

A system with feedback input uf, process noise input uw and tracked output ym:

A set of noise covariance matrices cvs and regulator weights wts:

The LQG tracking controller:

An unstable system:

A set of noise covariance matrices cvs and regulator weights wts:

The LQG regulator:

The open- and closed-loop poles:

The stable closed-loop and unstable open-loop poles are on the left- and right-hand sides of the s plane:

Scope  (33)

Basic Uses  (4)

A system with one feedback input uf and one noisy measurement ym:

The input covariance matrix cvs is empty because there are no noisy inputs:

A set of weights wts for the states and feedback input:

Compute the regulator:

Compute the regulator from a full system specification sspec:

A system with one feedback input uf, one noisy input uw and one noisy measurement ym:

A set of covariance matrices cvs and weights wts:

Compute the regulator:

A system with an exogenous deterministic input ue as well:

A set of covariance matrices cvs and weights wts:

Compute the regulator:

A general stochastic system:

A set of covariance matrices cvs and weights wts:

Compute the regulator:

Plant Models  (7)

Continuous-time StateSpaceModel:

Discrete-time StateSpaceModel:

Descriptor StateSpaceModel:

AffineStateSpaceModel:

NonlinearStateSpaceModel:

SystemModel:

A SystemModel with a noisy input:

The system specification:

A regulator design:

Properties  (14)

By default, LQGRegulator returns the controller comprising the estimator and regulator:

Assemble the LQGRegulator:

The LQGRegulator model:

The feedback gains:

The feedback gains model:

The model used to compute the feedback gains:

The estimator gains:

The model of the state estimator:

The model used to compute the estimator gains:

For nonlinear systems, the model used to design the estimator is the nonlinear state-space model:

The model to design the feedback gains is linear:

It is essentially the Taylor linearized state-space model:

The controller is the estimator and feedback gains in series:

The computed controller is the same:

The closed-loop system:

The closed-loop poles:

The design method:

Properties related to the input model:

Get the controller data object:

The list of available properties:

The value of a specific property:

Tracking  (5)

Design a tracking controller:

The closed-loop system tracks the reference signal :

Design a tracking controller for a discrete-time system:

The closed-loop system tracks the reference signal :

Track multiple outputs:

The closed-loop system tracks two different reference signals:

Compute the controller effort:

The controller model:

The controller inputs:

The controller effort:

Track a desired reference signal:

The reference signal is of order 4:

And a decaying sinusoid:

Design a controller to track one output of a first-order system:

The dimensions of the state weighting matrix qq are k+m q:

Compute the controller:

The closed-loop system tracks the reference:

Closed-Loop System  (3)

Assemble the closed-loop system for a nonlinear plant model with one disturbance input:

A set of noise covariance, regulator weight matrices:

The closed-loop system:

The closed-loop system with a linearized model:

Compare the response of the two systems:

Assemble the merged closed loop of a plant with an LQGRegulator:

A set of noise covariance, regulator weight matrices:

The merged closed-loop system:

The unmerged closed-loop system:

When merged, it gives the same result as before:

Explicitly merge the closed-loop system:

Create a closed-loop system with a desired name:

The closed-loop system has the specified name:

The name can be directly used in other functions:

Applications  (11)

Mechanical Systems  (3)

Regulate a tank’s turret angle from the azimuth:

A model of the system:

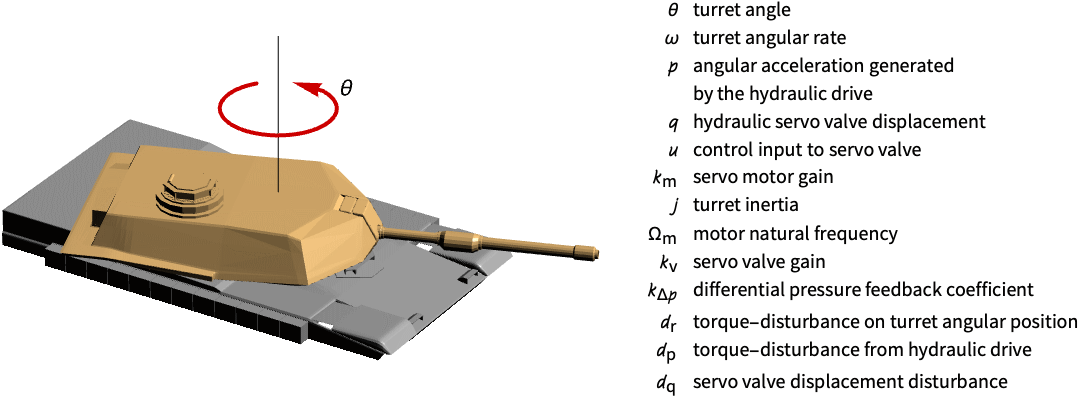
The turret’s orientation is unregulated to a initial disturbance in the states:

Set the system specifications:

Specify a set of process covariance matrices and LQ regulator weights:

Compute the LQG regulator:

Obtain the closed-loop system:

Create a noisy signal to simulate the process noise:

And measurement noise:

The turret’s angle is regulated:

Obtain the controller model:

Assess the control effort:

Regulate the motion of a robot arm:

A model of the system:

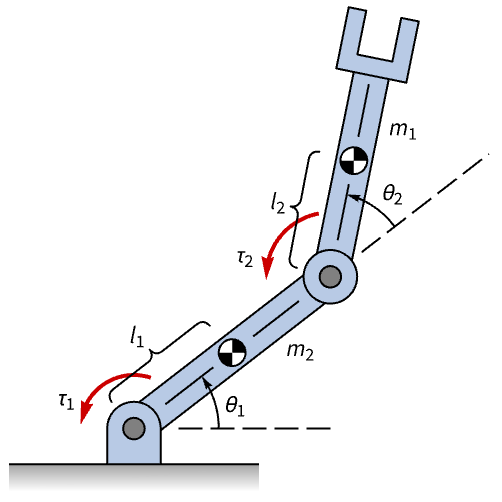
Without a controller, the motion of the arm is not regulated:

A set process covariance matrices and LQ regulator weights:

Compute the LQG controller:

Obtain the closed-loop system:

Generate a noisy signal to simulate the sensor noise:

The motion of the arm is controlled:

Obtain the controller model:

Assess the control effort:

Reject the disturbance on a gantry crane's load:

A model of the system:

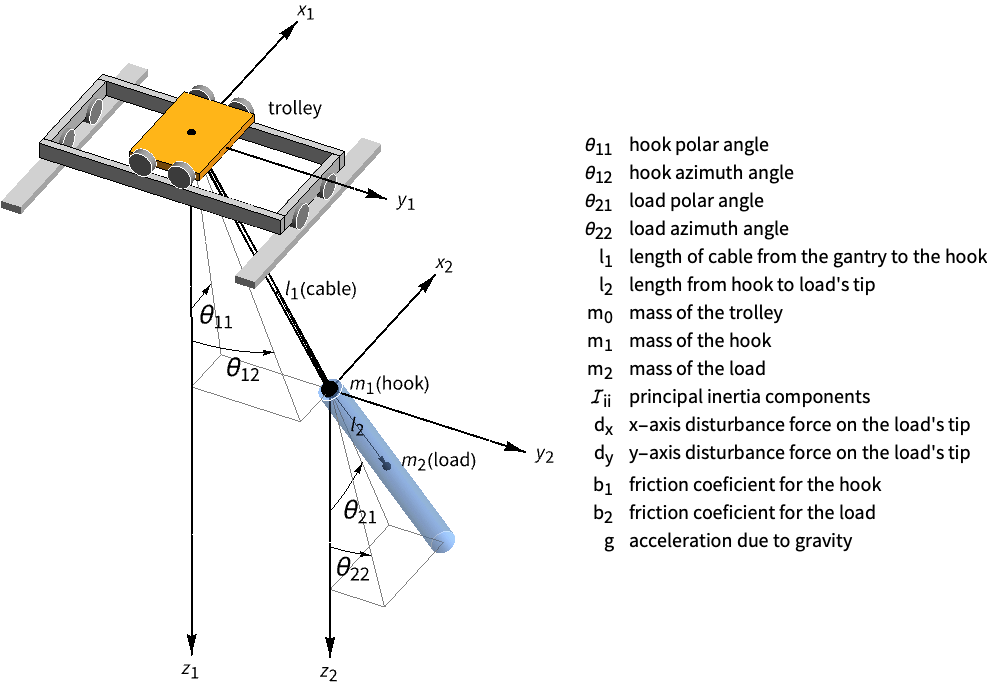
A disturbance force on the gantry causes the load to swing back and forth:

The design specification:

A set of noise covariance matrices:

A set of state and control weight matrices:

Compute the LQG controller:

Obtain the closed-loop system:

Generate a noisy signal to simulate the process noise:

And another for the sensor noise:

The disturbance is rejected and the oscillations are damped:

Obtain the controller model:

The control effort:

Aerospace Systems  (3)

Regulate the roll and yaw motions of a rigid spacecraft:

A model of the system:

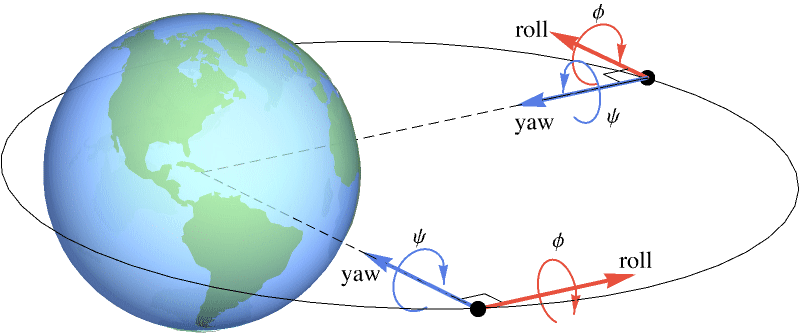
The open-loop response is unregulated:

Set the system specification:

A set of covariance and weight matrices for the LQG design:

Compute the LQG regulator:

Obtain the closed-loop system:

Generate a noisy signal to simulate the process noise:

And another for the sensor noise :

The satellite's orbit is regulated by the controller:

Obtain the controller model:

The control effort:

Reject a disturbance pushing a satellite away from the Lagrange point L1:

A model of the satellite:

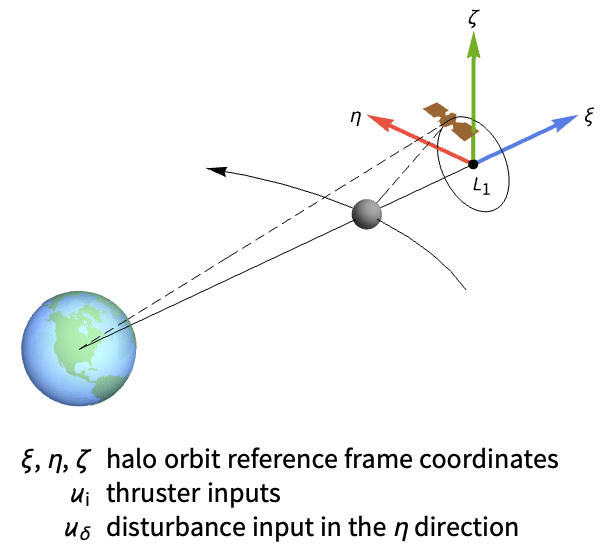
The satellite’s orbit is unstable to an initial disturbance in the η state:

At least thruster u_3 and another thruster are necessary to control the satellite:

Set the system specifications:

A set of process covariance matrices and LQ control weights:

Compute the LQG regulator:

Obtain the closed-loop system:

Generate a noisy signal to simulate the process noise:

And three for the measurement noises:

The satellite’s orbit is regulated for an initial disturbance in the η state:

Obtain the controller model:

Compute the control effort to reject the disturbance on the η state:

Stabilize the pitch and yaw of a helicopter model:

A model of the system:

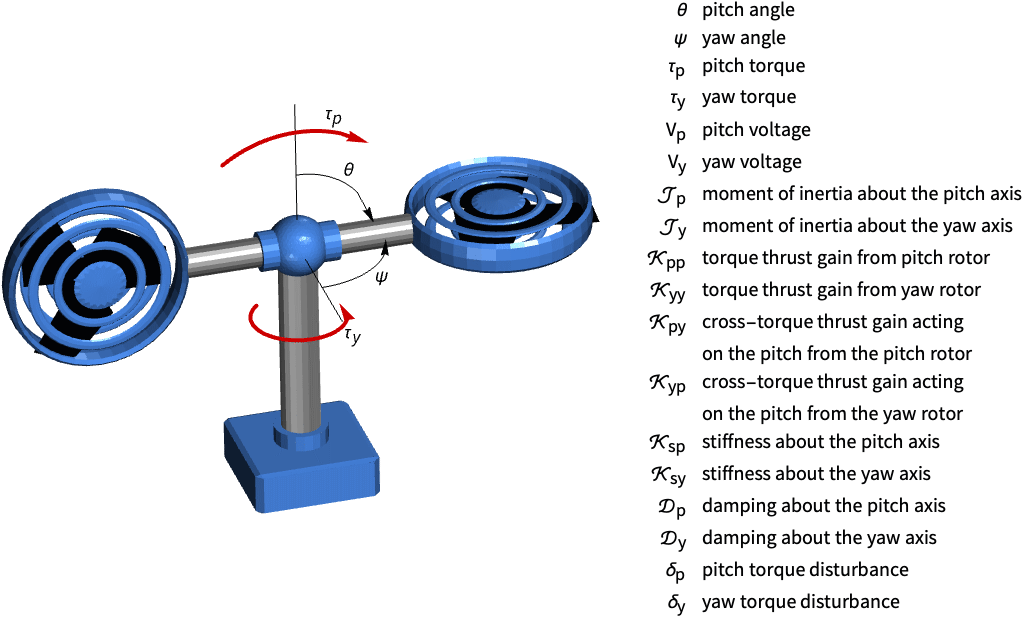
Discretize the system with a sampling time of :

A step input to the pitch motor affects the pitch and yaw simultaneously:

As does a step input to the yaw motor:

Set the feedback inputs to the yaw and pitch motor voltages:

A set of covariance matrices:

A set of state and control weight matrices:

Compute the LQG regulator:

Obtain the closed-loop system:

Generate two noisy signals to simulate the process noises for the pitch and yaw:

And another two for the pitch and yaw position sensors:

The closed-loop system’s pitch step response is stabilized:

As is the yaw step response:

Obtain the controller model:

Assess that the control effort is within the ±24V limits:

Marine Systems  (1)

Dampen the roll dynamics of a ship:

A model of the roll dynamics:

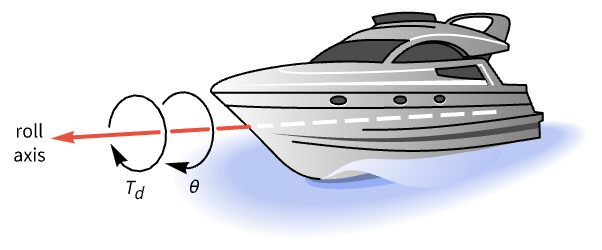
The step response is highly oscillatory:

The Bode plot reveals a low frequency response peak which causes the oscillations:

Obtain a state-space representation of the system:

Design an LQG controller to dampen the oscillations:

Obtain the closed-loop system:

Generate a noisy signal to simulate the noise in the pitch measurement:

The oscillations are damped:

The frequency responses of the open- and closed-loop systems shows the attenuated peak:

The controller model:

The control effort expended by the rudder:

Biological Systems (1)

Stabilize a population of lynx and hares:

A model of the system:

The lynx population is eliminated with a growth rate of zero:

Specify the system specification and a set noise covariance matrices and control weights:

Compute the LQG controller:

Obtain the closed-loop system:

Generate a noisy signal to add uncertainty in the population measurement:

The closed-loop response results in a stable cyclic response:

The parametric plot demonstrates the limit-cycle behaviour:

Obtain the controller model:

The control effort reveals the equilibrium values for the hare and lynx growth rates:

Economic Systems (1)

Stabilize an economic model:

The Samuelson economic model:

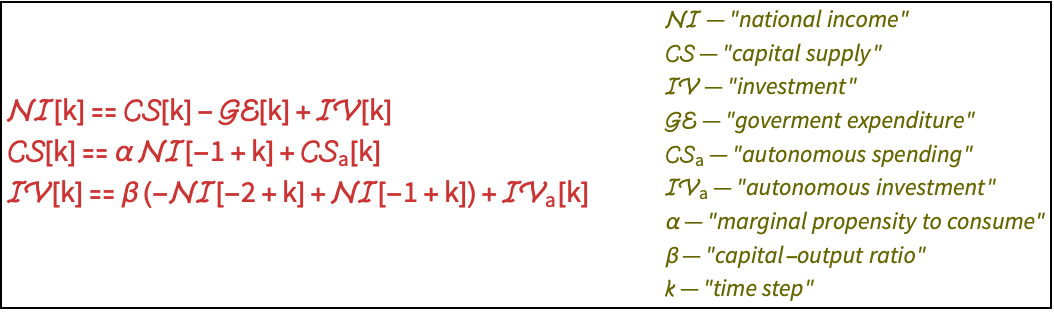
A disturbance to the consumer spending causes the economic model to become unstable:

A set of process covariance matrices and LQG control weights:

Compute an LQG controller that stabilizes the economic model:

Obtain the closed-loop system:

Generate measurement noise:

The national income reaches an equilibrium point:

Obtain the controller model:

Compute the government spending and autonomous consumption and investment:

Chemical Systems  (1)

Improve the performance of a CSTR for the decomposition reaction :

A model of the system:

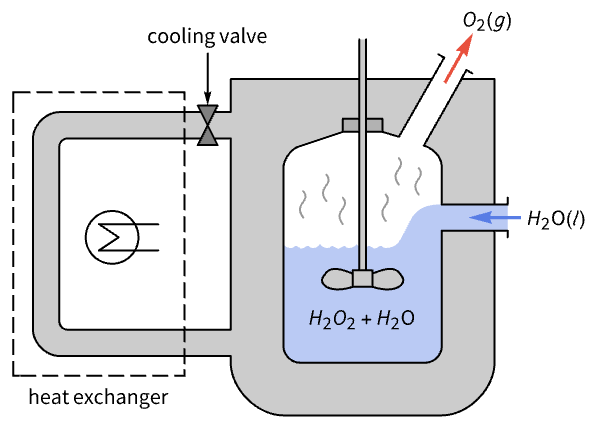
The system has two poles close to the imaginary axis:

This results in a sluggish response to a temperature perturbation:

Specify the system specification and a set of covariances matrices and control weights:

Compute the LQG controller:

Obtain the closed-loop system:

The closed-loop poles are further from the imaginary axis:

Generate a noisy signal to simulate the process noise:

The response to a temperature perturbation is faster:

Obtain the controller model:

Compute the control effort:

Electrical Systems  (1)

Regulate the speed of a DC motor:

A model of the system:

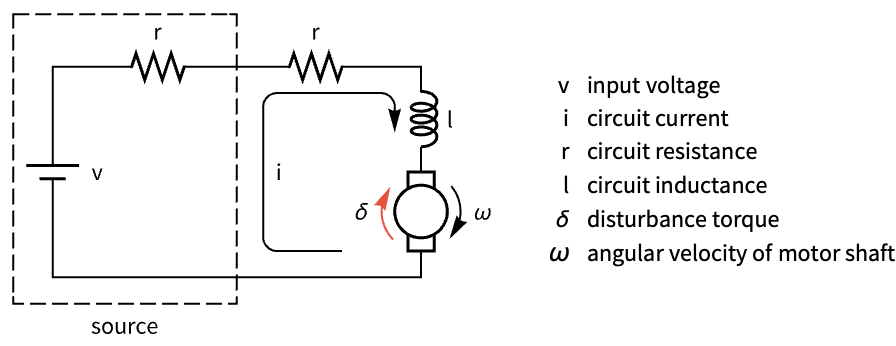
Discretize the model with a sampling period of 0.1:

Simulate the open-loop response to a torque disturbance:

Specify the system specification and a set of covariances matrices and control weights:

Compute the LQG controller:

Obtain the closed-loop system:

Generate a noisy signal to simulate the process noise:

And another for the sensor noise:

The inputs to the closed-loop system:

The closed-loop response tracks the reference value:

Obtain the controller model:

The controller inputs:

The control effort is less than v:

Properties & Relations  (8)

The closed-loop poles are the poles of the estimator and regulator:

The closed-loop poles:

The poles of the estimator subsystem:

The poles of the regulator subsystem:

The estimator and regulator poles together comprise the closed-loop poles:

The closed loop from the exogenous input to the measurement is an output feedback system:

The LQGRegulator:

The estimator regulator model:

The addition and comparator blocks:

The closed-loop system from to with the measurement noise :

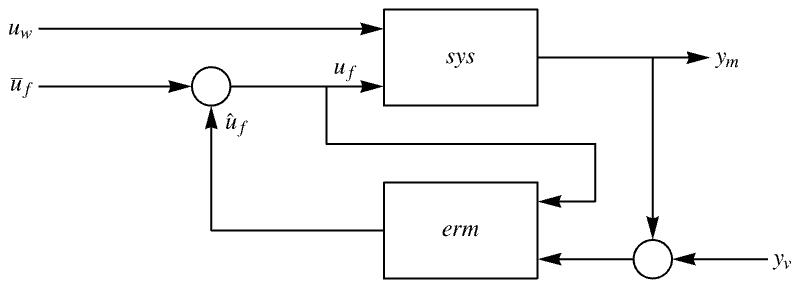
It can also be obtained as a property:

They are the same:

The closed-loop system from to :

The closed loop from the measurement noise to the measurement is a unity feedback system:

The LQGRegulator:

The transfer function of the closed-loop system from to y_(m):

The controller model with the reference input set to zero:

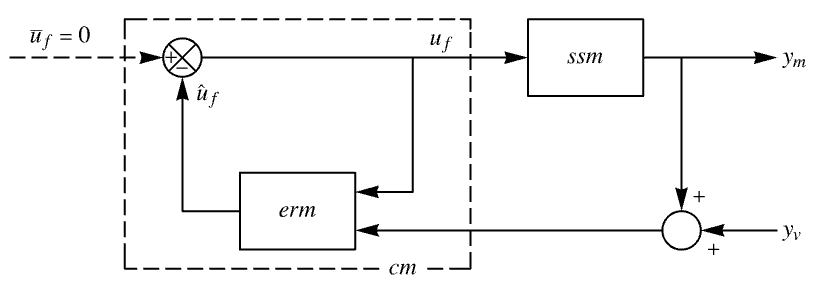
The transfer function of the positive unity feedback system from to y_(m):

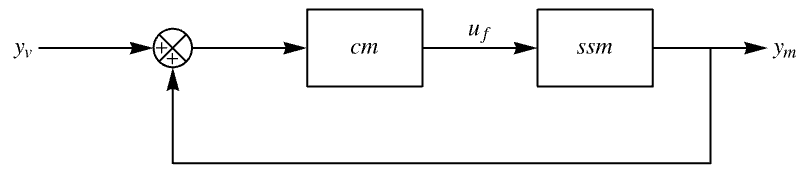
It is the same as the one obtained directly:

An LQGRegulator can be assembled using EstimatorRegulator:

Compute a set of optimal estimator gains:

And a set of optimal regulator gains:

Assemble the LQGRegulator using EstimatorRegulator:

LQGRegulator gives the same result:

Construct an LQG regulator from the Kalman estimator and the optimal state-feedback gains model:

The Kalman estimator:

The feedback gains model:

Assemble the estimator regulator model manually:

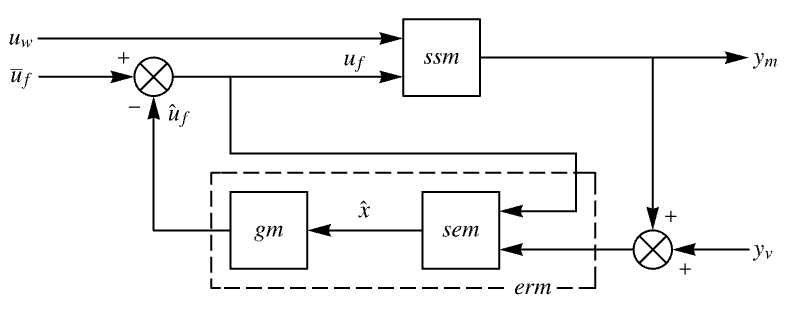
LQGRegulator gives the same result:

The performance of an LQR controller is better than an equivalent LQG controller:

The closed-loop system with an LQR controller:

The closed-loop system with an LQG controller:

The LQR's response is better than the LQG's:

An LQG controller is less robust than an LQR controller:

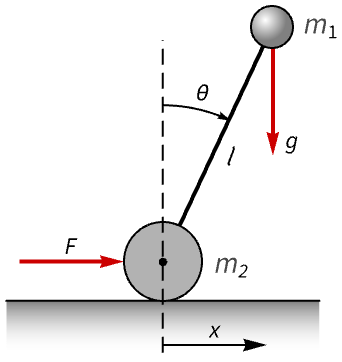
A model of an inverted pendulum on a cart:

The system specifications:

A set of noise covariance and control cost matrices:

The LQG controller:

The LQR controller:

The LQG closed-loop systems for the nominal and a perturbed system:

The closed-loop systems for the LQR controller:

The closed-loop response of the system with the LQG:

The LQR is more robust with less variation between the nominal and perturbed responses:

The performance of the LQG controller can be improved by tuning the covariance matrices:

The closed-loop system with the above specifications:

The closed-loop system with a tuned set of covariance matrices:

Tuning the covariance matrices results in an improved response:

Wolfram Research (2010), LQGRegulator, Wolfram Language function, https://reference.wolfram.com/language/ref/LQGRegulator.html (updated 2023).

Text

Wolfram Research (2010), LQGRegulator, Wolfram Language function, https://reference.wolfram.com/language/ref/LQGRegulator.html (updated 2023).

CMS

Wolfram Language. 2010. "LQGRegulator." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/LQGRegulator.html.

APA

Wolfram Language. (2010). LQGRegulator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LQGRegulator.html

BibTeX

@misc{reference.wolfram_2023_lqgregulator, author="Wolfram Research", title="{LQGRegulator}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LQGRegulator.html}", note=[Accessed: 19-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_lqgregulator, organization={Wolfram Research}, title={LQGRegulator}, year={2023}, url={https://reference.wolfram.com/language/ref/LQGRegulator.html}, note=[Accessed: 19-April-2024 ]}