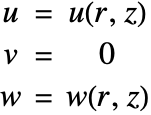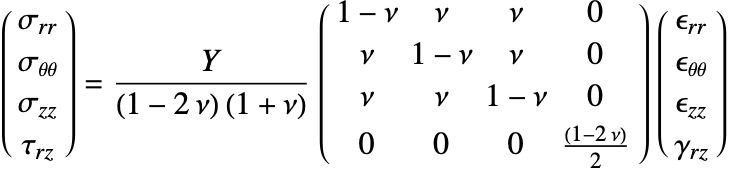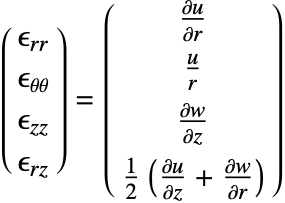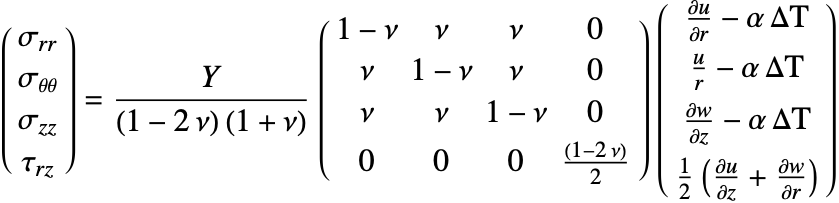Thermal and Structural Analysis of a Disc Brake
| Introduction | 2D axisymmetric structural mechanics model |
| Multiphysics Model | Model extensions |
| Axisymmetric Heat Transfer equation | Nomenclature |
| Domain | References |
| 2D axisymmetric heat transfer model |
Introduction
A braking system is generally composed of a brake disc and two brake pads. When braking, the brake pads exerts pressure on the disc to decelerate it. In this process there is a transformation of mechanical energy to thermal energy due to the friction between the pads and the disc. This energy is then dissipated in the material of the disc causing a change in the temperature distribution 
in 
. This non-uniform temperature distribution in the brake disc induces thermal stresses due to thermal expansion [Adamowicz,2015].
This notebook demonstrated a transient thermal analysis to calculate the temperature distribution caused by braking, and a quasi-static thermal stress analysis. The geometry of the disc and brake pads are mostly rotationally symmetric and an axisymmetric analysis will be shown. The model shown is a simplified disc brake that has brake pads all around and that is based on [Adamowicz,2015]. The rotationally symmetric assumption is warranted by the fact that the disc rotates quickly compared to the size of the pads.
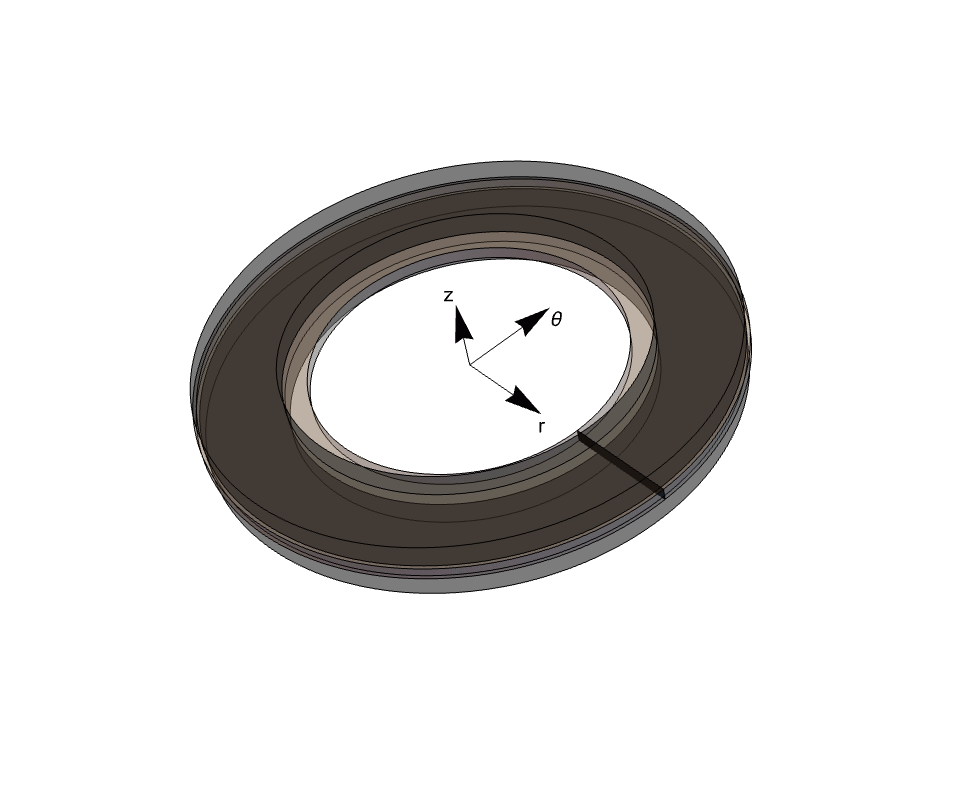
Revolving the black rectangular region which is the cross section through the brake disc around the 
-axis, the axis of revolution, we get the 3D model geometry as seen in the figure below.
Multiphysics Model
There are two physical domains involved in this application: the heat transfer model and the structural mechanics model. The coupling between the two models is one-way: The disc deformation depends on the temperature only. In this model we assume that influence of the deformed disc on the temperature field is small and thus not considered.
This type of problem is considered as a sequential multiphysics model, and will be solved in two steps.
First, the heat transfer model is solved to get the temperature distribution 
of the disc. Then, the structural mechanics model is constructed and the thermal stresses are computed at several solution times using the temperature distribution previously computed.
Axisymmetric Heat Transfer equation
The phenomenon of heat transfer is described by the heat equation, but in this example can be described by a special case of the heat equation: the axisymmetric form. This can be done because the domain and the boundary conditions are rotationally symmetric about the 
-axis. Using an axisymmetric model has the advantage that the computational cost in both time and memory is much less than in the case of solving a 3D heat transfer problem.
The axisymmetric heat transfer equation is given as:
where 
is the mass density in 
, 
is the specific heat capacity in 
and 
is the thermal conductivity in 
.
The axisymmetric heat equation uses a truncated cylindrical coordinate system in 2D with independent variables 
instead of the cylindrical coordinates 
. The cylindrical coordinate variable 
disappears because the system is rotationally symmetric about the 
-axis.
More information on the axisymmetric heat equation is given in the section Special Cases of the Heat Equation in the heat transfer overview monograph.
Axisymmetric Structural Mechanics Model
Just as in the heat transfer model, an axisymmetric structural solid mechanics simulation can be performed because the 3D solid is rotationally symmetric about the 
-axis. As in the 3D Cartesian model, the displacements are still called 
, 
and 
, but now 
is the displacement in the radial direction 
, 
the displacement in the angular direction 
, and 
in the axial direction 
. The assumption for the axisymmetric model is that there is no displacement in the 
-direction. This means that 
, and that 
and 
are independent of 
, leaving us with a truncated cylindrical coordinate system in 2D with independent variables 
.
Therefore, the constitutive equation can be given as:
where the strain vector is given by:
Now, to consider the thermal effects, an initial strain 
is included in the constitutive equation as follows:
In this case, 
represents a thermal strain which is given by:
where 
is the constant coefficient of linear thermal expansion (CLTE), measured in 
, 
is the temperature of the body in 
and 
is the reference temperature, also in 
at which there is no thermal strain in the body. A more detailed explanation can be found in the linear thermal expansion Solid Mechanics section.
So, at the end we finish with the following:
The axisymmetric case, additionally requires that the equilibrium equations be adapted to the cylindrical coordinate system too. More information on the axisymmetric solid mechanics approximation is given in the Axisymmetric Solid Mechanics section.
Domain
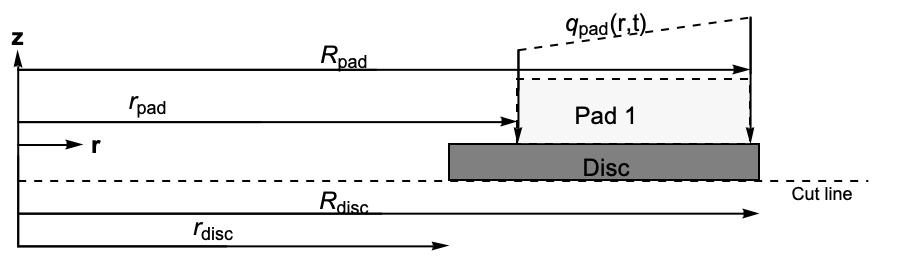
The domain of analysis in this case is an axially symmetric geometry, also known as body of revolution. The sketch below shows the simulation domain which is a rectangular region (disc) and one of the two brake pads.
In the following all length scales are given in meters 
. The simulation set up consists of a disc and a pad and there are various symmetries that are exploited. For one we have the rotational symmetry around the 
-axis which allows us to reduce the simulation domain only to a rectangular region corresponding to the axisymmetric section of the annular disc. A second symmetry is indicated by the cut line though the disc. Normally a brake system has a disc and two brake pads acting on the disc from both sides. Due to the second symmetry it is possible to half the disc thickness and only model one pad. The equation is then solved in the reduced disc and the pad is modeled as a boundary condition.
In the following all length scales are given in meters 
. The example models half the thickness of the disc 
, indicated by the dashed cut line, and the effect of one brake pad Pad 1 through the boundary condition. The geometry is described by the inner disc radius 
and outer disc radius 
, the inner radius 
and outer radius 
of the pad, the half thickness of the disc 
, and the thickness of the pad 
.
In a typical brake system, the outer radius of the disc 
is larger than the outer radius of the pad 
, but to stay consistent with [Adamowicz,2015], both outer radii were made equal. The first sketch also shows in which region the heat flow 
takes place.
for disc and 
for pad:To make use of boundary markers the boundary mesh is created manually, using ToBoundaryMesh. These markers can then be used to set up the boundary conditions on the geometry. Using markers can be simpler than specifying the formula for each boundary. This is explained further in the section Markers in the Element Mesh Generation.
Each of the marked edges will be used to position boundary conditions discussed later.
A max cell measure value was applied to the mesh to get a more accurate result.
2D axisymmetric heat transfer model
In the following section the heat transfer model will be solved to simulate the temperature field 
of the disc.
Parameters setup
In a next step we set up the material parameters and the 2D axisymmetric transient heat transfer equation. According to [Adamowicz,2015], the disc is made of cast iron ChNMKh and the pad is made out of cermet FMC-11. The mass density 
in 
, the specific heat capacity 
in 
and the thermal conductivity 
in 
of the disc will be defined.
Later, when the boundary conditions are specified it is more convenient to be able to access the parameter values directly then through their property names and thus we split the definition.
Next, we define the actual values.
The HeatTransferPDEComponent function can produce the axisymmetric form of the heat transfer equation. To do so the parameter "RegionSymmetry" is set to "Axisymmetric".
Boundary conditions
As mentioned above, the equation is only solved on the disc while the pad is modelled as a boundary condition, so there are two boundary conditions involved in this model that need to be defined.
One is a heat flux boundary condition to account for the heat flux that the pad generates in the region where is placed. The heat flux is active at the boundary element marker 3, that is from the inner radius of the pad 
to the outer radius of the pad 
. The heat flux is given by a function 
, which is the heat flux generated during a single braking process from a constant initial angular speed to a standstill and is described in [Adamowicz,2015].
The second boundary condition is a heat insulation condition and is active on the boundary parts marked with boundary element markers 1, 2, 4 and 5. A HeatInsulationValue produces a Neumann 0 value. As these are the natural default boundary conditions, these can be left out.
Apart from that, the yellow boundary with element marker 4 will be used differently in a later section where the model is extended further.
Model evaluation
What remains is to compute the numeric solution of the PDE with NDSolveValue.
Post-processing and Visualization
Plot the temperature changes on the contact surface of the disc 
during braking at key radial locations: at the inner and outer radius of disc and pad.
The resulting data is comparable to the Fig. 2. showed in [Adamowicz,2015].
See this note about improving the visual quality of the animation.
To visualize the full 3D solution from the axisymmetric model one can apply the interpolating function to visualize the data in a 3D domain. In other words, do a revolution plot of the data.
Use RegionPlot3D to make a plot showing the three-dimensional region in which pred is the equation of the annular disc.
2D axisymmetric structural mechanics model
In the following section the structural mechanics model is constructed and solved to show the thermally induced stresses.
Parameters setup
First, we set up the missing material parameters and the 2D axisymmetric solid mechanics PDE terms. The Young modulus 
in 
, the Poisson ratio 
, and the thermal expansion coefficient 
in 
of the disc will be defined.
The SolidMechanicsPDEComponent function can produce the axisymmetric form of the solid mechanics PDE terms. To do so the parameter "RegionSymmetry" in pars needs to be set to "Axisymmetric", which was already done above.
Here, the axisymmetric case is treated like a 3D set up. To make use of this, the dependent variable 
is set to 0 in the dependent variable set up. The actual computation, however, will still be done in 2D. This has several advantages. First, the retuned displacement will also have 
set and, secondly, both stress and strain will have the 
components set. Vector valued parameters are now specified as 3 component vectors.
Boundary Conditions
According to [Adamowicz,2015], the only constraint that has the disc is a zero displacement in the 
-direction at the disc bottom. Nevertheless, this constraint is insufficient to prevent rigid body motion, as mentioned here. A constraint for the displacement 
should be specified.
So, to prevent rigid body motion we will specify a zero displacement in the 
-direction at the disc left edge.
It should be mentioned that mechanical loads, like gravity, in the disc are not taken into account.
Model Evaluation
In this model, a quasi-static approach is taken to solve the structural solid mechanics model as in [Adamowicz,2015]. Quais-static means one solves the steady-state solid mechanics equation at a desired time of the temperature distribution solution. This can done repetitively at different times.
One might be inclined to use ParametricNDSolve for this task, but in current versions of the Wolfram language parametric functions can not take non constant arguments. This means that we need revert back to use NDSolve and replace the parameter with the interpolating function manually.
It is computationally more efficient to create a new interpolating function at each point time of interest. This is explained in more detail here.
:
with the thermal simulation result 
at different times:
Post-processing and Visualization
The objective of this simulation is to see the thermal stresses induced by the non-uniform temperature distribution. To obtain the thermal stresses, first, the strains need to be computed from the displacements, and then, the stresses can be recovered from the strains.
It is also possible to compute the von Mises stress.
Finally, a visualization is generated to show how much deformation occurred in the disc compared to the original one.
It should be noted that the results shown here differ from those of [Adamowicz,2015] because of the additional constraint to prevent rigid body motion in the radial direction that was added on the left edge of the disc.
Model extensions
The previous section introduced a simple disc brake PDE model. In this section the model is enhanced in two ways, to allow for more realistic simulations. First, the material parameters will be temperature dependent and, secondly, the thermal heat dissipation of the disc will be modeled by applying thermal convection and thermal radiation on the boundary.
Nonlinear material parameters
Depending on the carbon content in the disc, both the density and the thermal conductivity drop with increased temperature while the heat capacity increases with temperature. For all properties we use a simple linear model. For this we create use simple data points and find a linear fit to the material data. An alternative approach is to use an interpolating function as the material coefficients. This will also work, the find fit approach has the advantage that a time integration will be faster then when using the interpolating function approach, simply because the evaluation of the symbolic find fit model is more efficient than the lookup and interpolation in the interpolating function. Of course a higher order model for the fit could be used.
Convection and Radiation boundary conditions
A second improvement we'd like to make is to add a cooling mechanism. Here we'd like to consider both convective cooling and cooling by radiation.
The modeling approach we take here is that the area that is not covered by the brake pad exhibits a slightly large convective cooling then the area under the pad. Since the disc is rotation fast compared to the size of the pad one could go ahead and use the same heat transfer coefficient in both areas.
In the approach taken here we have radiative cooling in the area that is not covered by the brake pad.
In contrast, the area that is covered by the brake pad we also model radiative cooling but with a smaller emissivity.
Model evaluation
Visualization
Plot the temperature changes on the contact surface of the disc 
during braking at key radial locations to see how they differ from the simple disc brake PDE model.
Nomenclature
References
1. Adamowicz, A. (2015). Axisymmetric FE model to analysis of thermal stresses in a brake disk. Journal of Theoretical and Applied Mechanics (Poland), 53(2), 409–420. https://doi.org/10.15632/jtam-pl.53.2.357