ARIMAProcess
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v]
![]() 次差分が弱定常ARMAProcess[{a1,…,ap},{b1,…,bq},v]である,ARIMA(自己回帰和分移動平均)過程
次差分が弱定常ARMAProcess[{a1,…,ap},{b1,…,bq},v]である,ARIMA(自己回帰和分移動平均)過程 ![]() を表す.
を表す.
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},Σ]
(d,…,d)次差分が弱定常ベクトルARMAProcessである,ベクトルARIMA過程 (y1(t),… ,yn(t))を表す.
ARIMAProcess[{a1,…,ap},{d1,…,dn},{b1,…,bq},Σ]
(d,…,d)次差分が弱定常ベクトルARMAProcessである,ベクトルARIMA過程 (y1(t),… ,yn(t))を表す.
ARIMAProcess[{a1,…,ap},d,{b1,…,bq},v,init]
初期データ init のARIMA過程を表す.
ARIMAProcess[c,…]
定数 c のARIMA過程を表す.
詳細

- ARIMAProcessは離散時間・連続状態のランダム過程である.
- ARIMAProcess[…,d,…,v]には,次数 d(ただし d≥1)の多項式トレンドがある.
- ARIMA過程は差分方程式
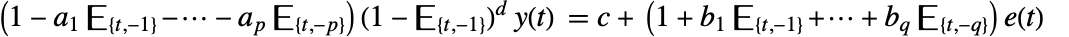 で説明される.
で説明される.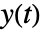 は状態出力,
は状態出力,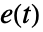 はホワイトノイズ入力,
はホワイトノイズ入力,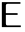 はシフト演算子であり,定数 c は指定がなければゼロであるとみなされる.
はシフト演算子であり,定数 c は指定がなければゼロであるとみなされる. - 初期データ init は,リスト{…,y[-2],y[-1]}として,あるいはタイムスタンプが{…,-2,-1}であると考えられる単一路TemporalDataオブジェクトとして与えることができる.
- スカラーARIMA過程には,実数係数 ai,bj,c,非負整数の和分次数 d,正の分散 v がなければならない.
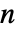 次元ベクトルARIMA過程には,次元が
次元ベクトルARIMA過程には,次元が 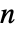 ×
×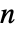 の実数係数行列 ai および bj,長さ
の実数係数行列 ai および bj,長さ 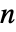 の実ベクトル c,非負整数の和分次数 di または非負整数の和分次数 d がなければならず,共分散行列 Σ は次元
の実ベクトル c,非負整数の和分次数 di または非負整数の和分次数 d がなければならず,共分散行列 Σ は次元 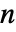 ×
×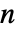 の正定値対称行列でなければならない.
の正定値対称行列でなければならない.- 定数がゼロであるARIMA過程は伝達関数
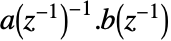 を持つ.ただし,
を持つ.ただし,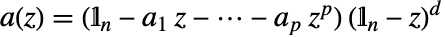 かつ
かつ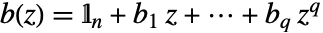 であり,
であり,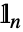 は
は 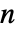 次元単位である.
次元単位である. - ARIMAProcess[p,d,q]は,自己回帰および移動平均の次数がそれぞれ p および q であり,和分次数が d である,EstimatedProcessおよび関連関数に使われるARIMA過程を表す.
- ARIMAProcessは,CovarianceFunction,RandomFunction,TimeSeriesForecast等の関数で使うことができる.
例題
すべて開くすべて閉じるスコープ (25)
基本的な用法 (9)
TimeSeriesModelを使って自動的に次数を求める:
推定法 (5)
ARIMAProcessの推定に使用できるメソッド:
スペクトル推定器では,PowerSpectralDensityの計算に使う窓を指定することができる:
過程スライス特性 (5)
1つの時間スライス分布(SliceDistribution):
CentralMomentおよびその母関数:
FactorialMomentは,記号次数では閉形式を持たない:
Cumulantおよびその母関数:
表現 (4)
アプリケーション (3)
データには線形のトレンドがある.これはUnitRootTestで確かめることができる:
1951年から1980年までの基線と比較した,地球の年間平均気温:
UnitRootTestで和分次数を求める:
特性と関係 (4)
ARIMAProcessはARMAProcessを一般化したものである:
ARIMAProcessはARProcessを一般化したものである:
ARIMAProcessはMAProcessを一般化したものである:
ARIMA過程は,離散ステップのWienerProcessに従う:
考えられる問題 (5)
複数の時間スライス特性は,記号タイムスタンプについては評価されないことがある:
FindInstanceを使って弱定常過程を求める:
厳密ではない母数のスライス分布特性は,記号時間については条件が不良であることがある:
ToInvertibleTimeSeriesは,常に存在するとは限らない:
単位円上にはTransferFunctionModelの零点が存在する:
おもしろい例題 (2)
三次元ARIMAProcessのシミュレーションを行う:
テキスト
Wolfram Research (2012), ARIMAProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/ARIMAProcess.html (2014年に更新).
CMS
Wolfram Language. 2012. "ARIMAProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ARIMAProcess.html.
APA
Wolfram Language. (2012). ARIMAProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ARIMAProcess.html