AbsoluteCorrelation
AbsoluteCorrelation[v,w]
ベクトル v とベクトル w の間の絶対相関を与える.
AbsoluteCorrelation[a,b]
行列 a と行列 b の絶対相互相関行列を与える.
行列 a の絶対相関行列を与える.
AbsoluteCorrelation[dist]
多変量記号分布 dist の絶対相関行列を与える.
AbsoluteCorrelation[dist,i,j]
多変量記号分布 dist の(i,j)番目の絶対相関を与える.
詳細

- AbsoluteCorrelation[v,w]は絶対相関の不偏推定を与える.
- AbsoluteCorrelationは,集中化された(ゼロ平均の)ベクトルについてCovarianceを計算する.
- AbsoluteCorrelationは,標準化された(ゼロ平均,単位分散)ベクトルについてCorrelationを計算する.
- 長さが
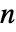 のベクトル
のベクトル  とベクトル
とベクトル 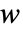 についての絶対相関推定AbsoluteCorrelation[v,w]は
についての絶対相関推定AbsoluteCorrelation[v,w]は 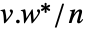 によって与えられる.
によって与えられる. - 次元が
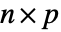 と
と  で列のインデックスが
で列のインデックスが 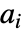 と
と 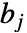 の行列
の行列 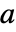 と
と 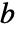 について,AbsoluteCorrelation[a,b]は要素が
について,AbsoluteCorrelation[a,b]は要素が 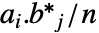 で与えられる
で与えられる  行列である,
行列である, -
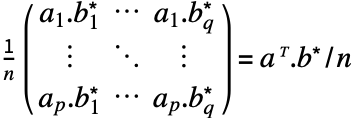
 列の行列
列の行列 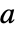 の場合,AbsoluteCorrelation[a]はAbsoluteCorrelation[a, a]で与えられる
の場合,AbsoluteCorrelation[a]はAbsoluteCorrelation[a, a]で与えられる 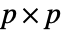 行列である.
行列である.- AbsoluteCorrelationはVectorQである任意のベクトルまたはMatrixQである任意の行列に使うことができる.
- AbsoluteCorrelation[dist,i,j]はExpectation[xixj,{x1,x2,…}∈dist]を与える.
- AbsoluteCorrelation[dist]は第(i,j)
 項目がAbsoluteCorrelation[dist,i,j]で与えられる絶対相関行列を与える.
項目がAbsoluteCorrelation[dist,i,j]で与えられる絶対相関行列を与える.
例題
すべて開くすべて閉じるスコープ (10)
データ (6)
構造化配列を使うことができる(ガイドを参照のこと):
アプリケーション (3)
AbsoluteCorrelationを使って線形関係を測ることができる:
AbsoluteCorrelationは単調関係しか検出することができない:
HoeffdingDを使ってさまざまな依存構造を検出することができる:
特性と関係 (8)
CovarianceおよびAbsoluteCorrelationは,ゼロ平均の分布について等しい:
CorrelationおよびAbsoluteCorrelationは,ゼロ平均および単位周辺分散について一致する:
AbsoluteCorrelationFunctionは,絶対相関行列の非対角項である:
リストについてのAbsoluteCorrelationFunctionは,絶対相関を使って計算することができる:
テキスト
Wolfram Research (2012), AbsoluteCorrelation, Wolfram言語関数, https://reference.wolfram.com/language/ref/AbsoluteCorrelation.html (2023年に更新).
CMS
Wolfram Language. 2012. "AbsoluteCorrelation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/AbsoluteCorrelation.html.
APA
Wolfram Language. (2012). AbsoluteCorrelation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AbsoluteCorrelation.html