AdjacentMeshCells

AdjacentMeshCells[mr,cellspec,d]

gives cells of dimension d adjacent to the cell specified by cellspec in the mesh mr.

Details

  • AdjacentMeshCells is also known as neighboring cells.
  • Typical uses include getting cell adjacencies and topological information in a mesh.
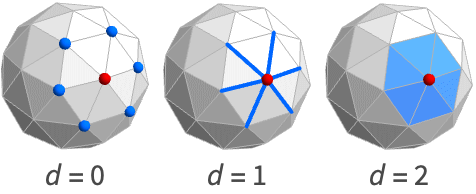
  • AdjacentMeshCells[mr,cellspec,d] returns a list of cell indices associated to the d-dimensional cells adjacent to cells specified by cellspec.
  • The following cell specifications cellspec can be used:
  • {d,i}cell with index i of dimension d
    {d,ispec}cells with index specification ispec of dimension d
    {dspec,…}cells of dimensions given by dspec
    h[{i1,…}]explicit cell with head h and vertex indices i1, …
    {c1,c2,…}list of explicit cells ci
  • The index specification ispec can have the following form:
  • icell index i
    {i1,i2,…}cells with indices ik
    Allall cells
    pattcells with indices matching the pattern patt
  • The dimension specification dspec can have the following form:
  • dexplicit dimension d
    Allall dimensions from 0 to geometric dimension of region
    pattdimensions matching the pattern patt

Examples

open allclose all

Basic Examples  (2)

A list of lines adjacent to the cell {0,2}:

Find all faces adjacent to the cells that match a pattern:

Scope  (5)

Basic Uses  (2)

Specify cells with index and dimension:

Pattern:

Explicit cells:

A list of cells:

Find the cells of different dimensions adjacent to the cell {0, 1}:

Mesh Regions  (2)

The AdjacentMeshCells of a MeshRegion in 2D:

Highlight the cells:

1D:

3D:

Highlight the cells:

The AdjacentMeshCells of a BoundaryMeshRegion:

Highlight the cells:

1D:

3D:

Highlight the cells:

Polygons & Polyhedra  (1)

AdjacentMeshCells of a Cube:

Simplex:

Polyhedron:

Triangle:

Polygon:

Line:

Applications  (8)

Basic Applications  (5)

Adjacent mesh cells of Triangle:

Adjacent mesh cells of Cube:

Adjacent mesh cells of MengerMesh:

Adjacent mesh cells of 3D boundary mesh:

Get the point adjacency of a Voronoi mesh:

Adjacency Queries  (1)

Use AdjacentMeshCells to find all the points that are connected to the point with cell index {0,1):

Polyhedra Operations  (1)

Use AdjacentMeshCells to compute the DualPolyhedron of a cuboid:

Get the adjacent faces for each point:

Compute the coordinates of the dual:

Construct the dual of the cube:

Topological Operations  (1)

Use MeshConnectivityGraph to test whether a mesh is connected:

Properties & Relations  (2)

The cell index {d, k} corresponds to the k^(th) cells of dimension d:

AdjacentMeshCells can be found using MeshConnectivityGraph:

Neat Examples  (1)

AdjacentMeshCells of a Menger mesh:

Wolfram Research (2020), AdjacentMeshCells, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacentMeshCells.html.

Text

Wolfram Research (2020), AdjacentMeshCells, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacentMeshCells.html.

CMS

Wolfram Language. 2020. "AdjacentMeshCells." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AdjacentMeshCells.html.

APA

Wolfram Language. (2020). AdjacentMeshCells. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AdjacentMeshCells.html

BibTeX

@misc{reference.wolfram_2024_adjacentmeshcells, author="Wolfram Research", title="{AdjacentMeshCells}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/AdjacentMeshCells.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_adjacentmeshcells, organization={Wolfram Research}, title={AdjacentMeshCells}, year={2020}, url={https://reference.wolfram.com/language/ref/AdjacentMeshCells.html}, note=[Accessed: 30-December-2024 ]}