AppellF1
AppellF1[a,b1,b2,c,x,y]
是双变量 Appell 超几何函数 ![]() .
.
更多信息

- AppellF1 属于Appell函数家族,它概括了超几何数列,解决了具有多项式系数的 Horn 偏微分方程组.
- 数学函数,适宜于符号和数值计算.
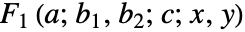 有一个通过超几何数列
有一个通过超几何数列 ![sum_(m=0)^inftysum_(n=0)^infty(TemplateBox[{a, {m, +, n}}, Pochhammer] TemplateBox[{{b, _, 1}, m}, Pochhammer] TemplateBox[{{b, _, 2}, n}, Pochhammer] )/(TemplateBox[{c, {m, +, n}}, Pochhammer]m! n!)x^m y^n sum_(m=0)^inftysum_(n=0)^infty(TemplateBox[{a, {m, +, n}}, Pochhammer] TemplateBox[{{b, _, 1}, m}, Pochhammer] TemplateBox[{{b, _, 2}, n}, Pochhammer] )/(TemplateBox[{c, {m, +, n}}, Pochhammer]m! n!)x^m y^n](Files/AppellF1.zh/3.png) 的主要定义,其在区域
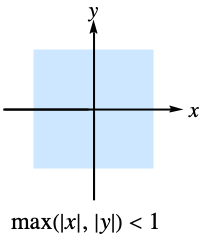
的主要定义,其在区域 ![max(TemplateBox[{x}, Abs],TemplateBox[{y}, Abs])<1 max(TemplateBox[{x}, Abs],TemplateBox[{y}, Abs])<1](Files/AppellF1.zh/4.png) 内是收敛的.
内是收敛的.- Appell F1 数列对其参数的实值的收敛区域如下:
- 一般来说,
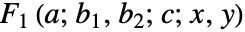 满足以下 Horn 偏微分方程组 »:
满足以下 Horn 偏微分方程组 »: 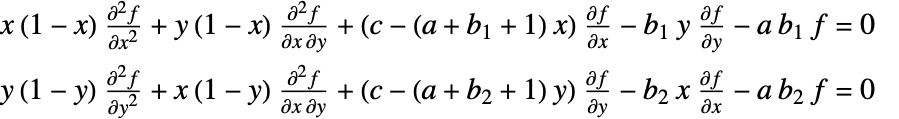 .
. - 当
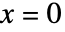 或
或 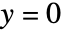 时,
时,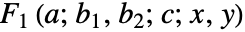 简化成为
简化成为 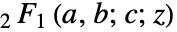 .
. - 对某些特殊自变量,AppellF1 自动计算出精确值.
- AppellF1 能够计算到任意数值精度.
- AppellF1[a,b1,b2,c,x,y] 在双变量复合
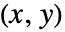 空间中的
空间中的 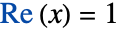 和
和 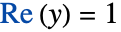 处有奇异线,并且沿
处有奇异线,并且沿 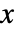 和
和 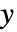 的从
的从 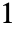 到
到 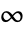 的射线上有分支切割.
的射线上有分支切割. - FullSimplify 和 FunctionExpand 包含用于 AppellF1 的变换法则.
范例
打开所有单元关闭所有单元基本范例 (8)
范围 (28)
数值计算 (6)
特殊值 (4)
函数属性 (9)
级数展开 (2)
属性和关系 (2)
巧妙范例 (1)
许多基本和特殊函数都是 AppellF1 的特例:
Wolfram Research (1999),AppellF1,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AppellF1.html (更新于 2023 年).
文本
Wolfram Research (1999),AppellF1,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AppellF1.html (更新于 2023 年).
CMS
Wolfram 语言. 1999. "AppellF1." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/AppellF1.html.
APA
Wolfram 语言. (1999). AppellF1. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AppellF1.html 年