AsymptoticSolve
AsymptoticSolve[eqn,yb,x->a]
计算方程 eqn 的解 y[x] 经过 {a,b} 的渐近逼近.
AsymptoticSolve[eqn,{y},x->a]
计算方程 eqn 的解 y[x] 在 x 靠近 a 处的渐近逼近.
AsymptoticSolve[eqns,{y1,y2,…}{b1,b2,…},{x1,x2,…}{a1,a2,…}]
计算方程式系统 eqns 的解 {y1[x1,x2,…],y2[x1,x2,…],…} 的渐进逼近.
AsymptoticSolve[eqns,…,{{x1,x2,…},{a1,a2,…},n}]
计算 n 阶的渐近逼近.
仅计算实参数的实值解.
更多信息和选项




- 渐近逼近通常用于求解无法找到精确解的问题,或者为计算、比较和解释寻求更简单的答案.
- AsymptoticSolve[eqn,…,xa] 计算 eqn 的渐近展开式中的首项. 用 SeriesTermGoal 可指定计算更多的项.
- 渐近逼近 yn[x] 常以和 yn[x]
 αkϕk[x] 的形式给出,其中 {ϕ1[x],…,ϕn[x]} 是当 xa 时的渐近尺度 ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x]. 则当 xa 时,结果满足 AsymptoticLess[y[x]-yn[x],ϕn[x],xa] 或 y[x]-yn[x]∈o[ϕn[x]].
αkϕk[x] 的形式给出,其中 {ϕ1[x],…,ϕn[x]} 是当 xa 时的渐近尺度 ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x]. 则当 xa 时,结果满足 AsymptoticLess[y[x]-yn[x],ϕn[x],xa] 或 y[x]-yn[x]∈o[ϕn[x]]. - 常见的渐近尺度包括:
-
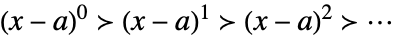
Taylor 尺度,当 xa 时 
Laurent 尺度,当 xa 时 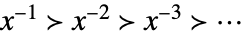
Laurent 尺度,当 x±∞ 时 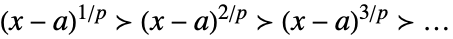
Puiseux 尺度,当 xa 时 - 用于表示渐近逼近的尺度是从问题中自动推断出来的,通常可以包含更多的奇异尺度.
- 中心坐标 a 和 b 可以为任意有限或无限大实数或复数.
- 阶数 n 必须为一个正整数,指定渐近解的近似阶数. 与多项式的次数无关.
- 方程组 eqns 可为方程的任意逻辑组合.
- 可以给出以下选项:
-
Assumptions $Assumptions 对参数的设定 Direction Automatic x 接近 a 的方向 GenerateConditions Automatic 是否给出与参数的条件有关的答案 Method Automatic 所用的方法 PerformanceGoal $PerformanceGoal 优化的目标 SeriesTermGoal Automatic 近似式的项数 - Direction 的可能设置包括:
-
Reals 或 "TwoSided" 从两个实方向 "FromAbove" 或 -1 从上面或较大的值 "FromBelow" 或 +1 从下面或较小的值 Complexes 从所有复方向 Exp[ θ] 从方向 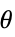
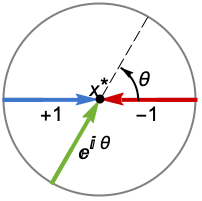
{dir1,…,dirn} 对变量 xi 分别使用方向 diri - 在 x* 处的 DirectionExp[ θ] 表示接近极限点 x* 的曲线的方向切线.
- 对于 a 的有限值,Automatic 设置表示从上面接近.
- 如果指定了域 Reals,则当 x 从 Direction 逼近 a 时,解为实数.
- GenerateConditions 的可能设置包括:
-
Automatic 只给出非通用条件 True 所有条件 False 不给出条件 None 如果需要条件则不经计算直接返回 - PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 当设置为 "Quality" 时,AsymptoticSolve 通常可以解出更多的问题或者产生更简单的结果,但是可能会耗费更多的时间和内存.
范例
打开所有单元关闭所有单元范围 (18)
二维空间中的一维解 (8)
n (5) 维空间中的一维解
选项 (9)
Assumptions (1)
用 Assumptions 为参数指定条件:
Direction (3)
默认情况下,AsymptoticSolve 当 x 从上面逼近 0 时的解:
GenerateConditions (3)
默认情况下,AsymptoticSolve 对能给出结果的情况产生条件:
当设置为 GenerateConditions->True 时,所有条件都要报告:
当设置为 GenerateConditions->None 时,AsymptoticSolve 只返回通常情况下有效的解:
如果需要非通用条件,AsymptoticSolve 不执行任何计算,直接返回:
SeriesTermGoal (1)
默认情况下,AsymptoticSolve[eqn,…,xa] 计算解的首项:
用 SeriesTermGoal 获得更多项:
应用 (12)
隐函数 (3)
方程 ![]() 隐式定义了
隐式定义了 ![]() 附近的两个不同的函数
附近的两个不同的函数 ![]() . 计算这两个函数在
. 计算这两个函数在 ![]() 附近的三阶渐近近似:
附近的三阶渐近近似:
AsymptoticSolve 返回的两个表达式是精确解的级数:
曲线 ![]() 无限多次穿过直线
无限多次穿过直线 ![]() . 在通过垂直线测试(任何垂直线只与曲线相交一次;没有垂直线多次与该部分相交)的部分,隐式定义了一个函数:
. 在通过垂直线测试(任何垂直线只与曲线相交一次;没有垂直线多次与该部分相交)的部分,隐式定义了一个函数:
方程的级数解 (2)
曲线的渐近近似 (3)
文本
Wolfram Research (2019),AsymptoticSolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AsymptoticSolve.html (更新于 2020 年).
CMS
Wolfram 语言. 2019. "AsymptoticSolve." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/AsymptoticSolve.html.
APA
Wolfram 语言. (2019). AsymptoticSolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AsymptoticSolve.html 年