AsymptoticSum

AsymptoticSum[f,x,xx0]

计算不定和 的渐进逼近，其中 x 以 x0 为中心.

AsymptoticSum[f,{x,a,b},αα0]

计算确定和 的渐进逼近，其中 α 以 α0 为中心.

AsymptoticSum[f,…,{ξ,ξ0,n}]

计算 n 阶渐近逼近.

更多信息和选项

  • 和的渐近逼近亦被称为渐近展开式和摄动展开式. 也可用计算其中一些式子的特定方法来称呼它们，如 Euler–Maclaurin 方法、分部求和法等.
  • 渐近逼近通常用于计算无法找到精确结果的求和问题，或者为计算、比较和解释寻求更简单的答案.
  • AsymptoticSum[f,…,xx0] 计算 f 的渐近展开式的首项. 用 SeriesTermGoal 可指定计算更多的项..
  • 如果精确结果为 g[x]，在 x0 处的 n 阶渐近逼近为 gn[x]，那么当 xx0 时，结果为 AsymptoticLess[g[x]-gn[x],gn[x]-gn-1[x],xx0] 或 g[x]-gn[x]∈o[gn[x]-gn-1[x]].
  • 渐近逼近 gn[x] 常以和 gn[x]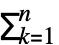αkϕk[x] 的形式给出，其中 {ϕ1[x],…,ϕn[x]} 是当 xx0 时的渐近尺度 ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x]. 则当 xx0 时，结果为 AsymptoticLess[g[x]-gn[x],ϕn[x],xx0] 或 g[x]-gn[x]∈o[ϕn[x]].
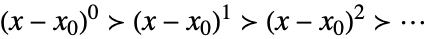
  • Taylor 尺度，当 xx0 时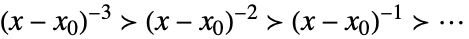
    Laurent 尺度，当 xx0 时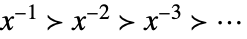
    Laurent 尺度，当 x±∞ 时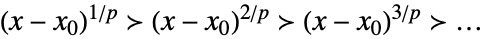
    Puiseux 尺度，当 xx0 时
  • 用于表示渐近逼近的尺度是从问题中自动推断出来的，通常可以包含更多的奇异尺度.
  • 中心点 α0 可为任意有限或无限大实数或复数.
  • 阶数 n 必须为一个正整数，指定渐近展开式的近似阶数. 与多项式的次数无关.
  • 可以给出以下选项：
  • AccuracyGoalAutomatic寻求的绝对准确度
    Assumptions$Assumptions对参数的设定
    GenerateConditionsAutomatic是否给出与参数的条件有关的答案
    GeneratedParameters None怎样命名生成的参数
    MethodAutomatic所用的方法
    PerformanceGoal$PerformanceGoal优化目标
    PrecisionGoalAutomatic寻求的精度
    Regularization None所使用的正则化方案
    SeriesTermGoalAutomatic近似式的项数
    WorkingPrecisionAutomatic内部计算中使用的精度
  • PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 当设置为 "Quality" 时， AsymptoticSum 通常可以解出更多的问题或者产生更简单的结果，但是可能会耗费更多的时间和内存.

范例

打开所有单元关闭所有单元

基本范例  (3)

计算和的渐近逼近的首项：

计算和的渐近展开式：

与 n 取较大值时的精确值相比较：

计算和 (sum) 关于一个参数的渐近展开式：

计算要求的展开式：

与 a 取较小值时的精确值相比较：

范围  (13)

不定和  (5)

计算有理和的渐近展开式：

与 Sum 给出的结果相比较：

多项式指数和的渐近展开式：

与 Sum 给出的结果相比较：

超几何和的渐近展开式：

估计在一个点的值：

与 NSum 给出的结果相比较：

有理指数和的渐近展开式：

验证结果：

PolyGamma 和的渐近展开式：

确定和  (4)

计算有理和的渐近展开式：

与 NSum 给出的结果相比较：

有理指数和的渐近展开式：

与 NSum 给出的结果相比较：

计算超几何和的渐近展开式：

与精确结果相比较：

HarmonicNumber 和的渐近展开式：

与 NSum 给出的结果相比较：

参数和  (4)

计算关于一个参数的渐近展开式：

验证结果：

计算无限指数和的渐近展开式：

与精确结果相比较：

与 Zeta 相关的和的渐近展开式：

与数值近似相比较：

交替高斯指数和的渐近展开式：

与数值近似相比较：

选项  (3)

GeneratedParameters  (1)

为不定和产生一个任意常数：

任意常数的默认值是 0：

Regularization  (2)

使用 Abel 正则化计算发散和的渐近展开式：

使用 Borel 正则化计算发散和的渐近展开式：

应用  (9)

计算有限和的近似值：

计算 n 增大时的数值近似：

与由 Sum 给出的精确结果相比较：

计算定积分的黎曼和近似：

计算 n 取较大值时的近似：

与 Integrate 给出的结果相比较：

用 DiscreteLimit 获取精确结果：

绘制近似值和精确值：

计算反常积分的数值近似：

计算 n 取较大值时的近似：

与 NIntegrate 给出的结果相比较：

证明 ：

与精确结果的展开式相比较：

计算 的渐近展开式：

比较 时的近似值和精确值：

计算高斯和的渐近逼近：

比较 时的近似值和精确值：

计算有理和的一阶渐近逼近：

有理指数和：

超几何和：

证明当 n 趋近于 Infinity 时 渐近逼近于 1/n：

用 AsymptoticEquivalent 验证上述等价性：

用从 Sum 所得的结果进行验证：

计算二项式和的渐近逼近：

比较 时的近似值和精确值：

属性和关系  (3)

AsymptoticSum 计算给定阶数的和：

通过 Sum 用解析式计算和：

用 NSum 计算数值近似：

Wolfram Research (2019)，AsymptoticSum，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AsymptoticSum.html （更新于 2020 年）.

文本

Wolfram Research (2019)，AsymptoticSum，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AsymptoticSum.html （更新于 2020 年）.

CMS

Wolfram 语言. 2019. "AsymptoticSum." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/AsymptoticSum.html.

APA

Wolfram 语言. (2019). AsymptoticSum. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AsymptoticSum.html 年

BibTeX

@misc{reference.wolfram_2024_asymptoticsum, author="Wolfram Research", title="{AsymptoticSum}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticSum.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_asymptoticsum, organization={Wolfram Research}, title={AsymptoticSum}, year={2020}, url={https://reference.wolfram.com/language/ref/AsymptoticSum.html}, note=[Accessed: 15-November-2024 ]}