Ball

Ball[p]

点 p を中心とする単位球体を表す．

Ball[p,r]

半径 r で点 p を中心とする球体を表す．

Ball[{p1,p2,…},r]

半径 r の球体の集合を表す．

詳細とオプション

  • Ballは，中心区間，円板，ボール，超球体としても知られている．
  • Ballは，幾何領域および地理プリミティブとして使うことができる．
  • Ball[]はBall[{0,0,0}]に等しい．
  • 整数 n についてのBall[n]は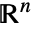，における単位球体であるBall[{0,…,0}]に等しい．
  • Ballは，塗り潰された球体{x|TemplateBox[{{x, -, p}}, Norm]<=r}を表す．領域は，長さ の点 p について 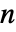次元である．
  • Ballでは，点 p が内の任意の点で，r が任意の正の実数でよい．
  • BallはGraphicsおよびGraphics3Dで使うことができる．
  • グラフィックスでは，点 p, piおよび半径 r は，Scaled式およびDynamic式でよい．
  • グラフィックスの描画は，FaceForm，EdgeForm，Specularity，Opacity，色等の指示子の影響を受ける．
  • Ball[{p1,p2,…},{r1,r2,…}]は，中心 pi，半径 riの球面の集合を表す．

予備知識

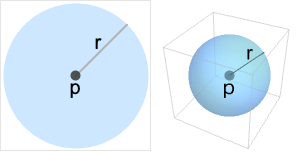
  • Ballは， 次元空間の球体を表すグラフィックスおよび幾何のプリミティブである．Ball[p,r]はTemplateBox[{}, Reals]^n内の，中心が p で半径が r である（塗り潰された）球体{x:TemplateBox[{{x, -, p}}, Norm]<=r}を表す．r は任意の非負の実数でよく，p は任意の正の距離 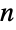を持つ．略記形式のBall[p]はBall[p,1]に，
    Ball[n]はBall[ConstantArray[0, n],1]に等しく，Ball[]を評価すると自動的にBall[{0,0,0}]になる．
  • 半径 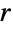が等しい球体オブジェクトの集合（複数の球体）は，Ball[{p1,…,pk},r] を使って効率的に表現することができ，半径が異なる球体はBall[{p1,…,pk},{r1,…,rk}]で表すことができる．
  • Ballオブジェクトは，GraphicsおよびGraphics3Dを使って，それぞれ二次元および三次元で視覚的にフォーマットすることができる．グラフィックス内のBallオブジェクトの外観は，辺指示子EdgeForm（二次元）あるいは面指示子FaceForm（三次元），Red等の色指示子，不透明度／透明度の指示子のOpacityおよびSpecularity，スタイルオプションAntialiasingを指定して変更することができる．
  • Ballは，計算を行うべき領域指定にも使うことができる．例えば，Integrate[1,{x,y,z}∈Ball[{0,0,0},r]]とVolume[Ball[{0,0,0},r]]はどちらも，半径 の三次元の球体の体積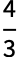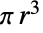を返す．
  • Ballは数多くの他のシンボルと関連がある．Sphereは，RegionBoundary[Ball[{x,y,z},r]]を使って計算できる球体の境界を表す．Ballは任意次元におけるIntervalとDiskの一般化であり，Ellipsoidは，すべての 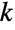についてBall[{p1,…,pk},1]がEllipsoid[{p1,…,pk},ConstantArray[1,k]]に等しいという意味でBallの一般化である．SphericalShellは，大きい球から同心の小さい球体を除いて得られる塗り潰された殻を与える．3DのBallオブジェクトは，ImplicitRegion[(x-u)2+(y-v)2+(z-w)2≤r2,{u,v,w}]またはParametricRegion[a{Cos[θ]Sin[ϕ],Sin[θ]Sin[ϕ],Cos[ϕ]}-{x,y,z},{{θ,0,2π},{ϕ,0,π},{a,0,r}]として表される．SolidData["entity", "property"]あるいはEntityValue[Entity["Ball","entity"],"property"]を使って標準位置にある3Dの球体の計算済みの特性とその異体を求めることができる．ただし，"entity"は"Ball"または"HalfBall"である．

例題

すべて開くすべて閉じる

例  (2)

3Dにおける単位球体：

2Dにおける単位球体：

体積と重心：

スコープ  (22)

グラフィックス  (12)

指定  (4)

デフォルトは3Dの原点における単位球体である：

異なる次元の単位球体：

位置と半径が異なる球体：

半径が等しい複数の球体：

スタイリング  (4)

鏡面反射指数が異なる球体：

赤く輝く黒い球体：

Opacityは表面の不透明度を指定する：

2Dにおけるスタイリング：

座標  (4)

プロット範囲との割合で座標を指定する：

プロット範囲との割合で半径を指定する：

通常の座標からスケールされたオフセットを指定する：

点はDynamicでもよい：

領域  (10)

埋込み次元は球体がある空間の次元である：

幾何次元は形それ自体の次元である：

帰属判定：

点の帰属条件を得る：

体積：

重心：

点からの距離：

2D球体についての，最近点までの距離：

3D球体についての等距離等高線：

点からの符号付き距離：

2D球体までの符号付き距離：

領域内の最近点：

包み込んでいる球面までの最近点：

球体は有界である：

範囲を求める：

球体領域で積分する：

球体領域で最適化する：

球体領域内で方程式を解く：

アプリケーション  (3)

体積が の球体の最小表面積を求める：

密度が で与えられる球体領域の総質量を求める：

半径3cmの球体の中のカフェインの質量を求める：

カフェインの密度：

球体の体積：

球体中のカフェインの質量：

特性と関係  (5)

DiskはBallの特殊ケースである：

SphereはBallのRegionBoundaryである：

EllipsoidはBallを一般化したものである：

ImplicitRegionは任意のBallを表すことができる：

Ballはユークリッドノルムのノルム球体である：

おもしろい例題  (1)

ランダムな球体の集合：

Wolfram Research (2014), Ball, Wolfram言語関数， https://reference.wolfram.com/language/ref/Ball.html.

テキスト

Wolfram Research (2014), Ball, Wolfram言語関数， https://reference.wolfram.com/language/ref/Ball.html.

CMS

Wolfram Language. 2014. "Ball." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Ball.html.

APA

Wolfram Language. (2014). Ball. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ball.html

BibTeX

@misc{reference.wolfram_2024_ball, author="Wolfram Research", title="{Ball}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Ball.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ball, organization={Wolfram Research}, title={Ball}, year={2014}, url={https://reference.wolfram.com/language/ref/Ball.html}, note=[Accessed: 21-November-2024 ]}