Ball

Ball[p]

表示中心在点 p 的单位球.

Ball[p,r]

表示中心在点 p、半径为 r 的球.

Ball[{p1,p2,…},r]

表示半径为 r 的一组球.

更多信息和选项

  • Ball 也称作中心区间、圆盘、球和和超球.
  • Ball 可用作几何区域和图形基元.
  • Ball[] 等价于 Ball[{0,0,0}].
  • 对于整数 n，Ball[n] 等价于 Ball[{0,…,0}]，在 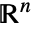中的单位球.
  • Ball 表示实心球 {x|TemplateBox[{{x, -, p}}, Norm]<=r}. 对于长度为 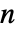的点 p，区域是 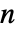维的.
  • Ball 允许 p 为 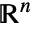中的任意点，r 为任意正实数.
  • Ball 可用于 Graphics 和 Graphics3D.
  • 在图形中，点 p、pi 和半径 r 可以是 Scaled 和 Dynamic 表达式.
  • 图形渲染受指令 FaceForm、EdgeForm、Specularity、Opacity 和颜色等影响.
  • Ball[{p1,p2,…},{r1,r2,…}] 表示中心为 pi、半径为 ri 的一组球体.

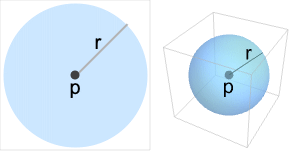
背景

  • Ball 是一个图形和几何基元，表示一个在 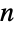维空间的球. 尤其是，Ball[p,r] 表示一个在 TemplateBox[{}, Reals]^n 中的（填充的）球 {x:TemplateBox[{{x, -, p}}, Norm]<=r}，其中心为 p，半径为 r，r 可以是任何非负实数，p 可以有任何正长度 . 速记形式 Ball[p] 等同于 Ball[p,1]，Ball[n] 等同于 Ball[ConstantArray[0, n],1]，其中 Ball[] 自动计算为 Ball[{0,0,0}].
  • 共同半径 的球对象（多个球）收集可以使用 Ball[{p1,…,pk},r] 高效表示，有多种半径的球可以用 Ball[{p1,…,pk},{r1,…,rk}] 表示.
  • Ball 对象可以分别使用 Graphics 和 Graphics3D 在二维和三维中进行可视格式化. 图形中的 Ball 对象外观的修改可以通过指定边指令 EdgeForm (2D) 或面指令 FaceForm (3D)，颜色指令例如，Red，透明度和镜面反射度 Opacity 和 Specularity，样式选项 Antialiasing.
  • Ball 也可以作为在其上执行计算的区域规范. 例如，Integrate[1,{x,y,z}∈Ball[{0,0,0},r]] 和 Volume[Ball[{0,0,0},r]] 均返回半径为 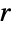的 3D 球的体积 .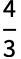
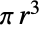  • Ball 还与其他符号相关. Sphere 表示球的边界，可以用 RegionBoundary[Ball[{x,y,z},r]] 计算. Ball 是 Interval 和 Disk 到任意维数的推广，Ellipsoid 是 Ball 的推广，在某种意义上，对于所有 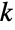，Ball[{p1,…,pk},1] 等同于 Ellipsoid[{p1,…,pk},ConstantArray[1,k]]. SphericalShell 给出了从较大的同心球的内部去除一个小球而获得的填充的壳. 3D 中的 Ball 对象可以表示为 ImplicitRegion[(x-u)2+(y-v)2+(z-w)2≤r2,{u,v,w}] 或 ParametricRegion[a{Cos[θ]Sin[ϕ],Sin[θ]Sin[ϕ],Cos[ϕ]}-{x,y,z},{{θ,0,2π},{ϕ,0,π},{a,0,r}]. 3D 球的预计算属性和其在标准位置上的变体可使用 SolidData["entity", "property"] 或 EntityValue[Entity["Ball","entity"],"property"]，其中"entity" 是 "Ball" 或 "HalfBall" 中的一个.

范例

打开所有单元关闭所有单元

基本范例  (2)

在三维中的单位球：

在二维中：

体积和质心：

范围  (22)

图形  (12)

指定  (4)

默认值是三维中原点处的一个单位球：

不同维度的单位球：

不同位置和半径的球：

相等半径的多个球：

样式化  (4)

具有不同镜面指数的球：

发红光的黑球：

Opacity 指定面的不透明度：

二维样式化：

坐标  (4)

以绘图范围分数的形式指定坐标：

以绘图范围分数的形式指定半径：

指定从普通坐标缩放的偏移量：

点可以是 Dynamic：

区域  (10)

嵌入维是球所在空间的维度：

几何维度是形状本身的尺寸：

成员测试：

得到点成员的条件：

体积：

质心：

到一个点的距离：

到二维球最近点的距离：

三维球的等距轮廓：

到一个点的带有正符号的距离：

到二维球的带有正符号的距离：

区域上的最近点：

到一个封闭球体的最近点：

球是有界的：

求它的范围：

在球的区域上积分：

在球的区域上最优化：

求解球的区域上的方程：

应用  (3)

求体积为 的球的最小表面积：

球区域的总质量，其密度由 给出：

求半径为3厘米的球中咖啡因的质量：

咖啡因的密度：

球的体积：

球中咖啡因的质量：

属性和关系  (5)

Disk 是 Ball 的特例：

Sphere 是 Ball 的 RegionBoundary：

Ellipsoid 是广义的 Ball：

ImplicitRegion 可以表示任何 Ball：

Ball 是欧几里德范数的范数球：

巧妙范例  (1)

随机球集合：

Wolfram Research (2014)，Ball，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Ball.html.

文本

Wolfram Research (2014)，Ball，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Ball.html.

CMS

Wolfram 语言. 2014. "Ball." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Ball.html.

APA

Wolfram 语言. (2014). Ball. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Ball.html 年

BibTeX

@misc{reference.wolfram_2024_ball, author="Wolfram Research", title="{Ball}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Ball.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ball, organization={Wolfram Research}, title={Ball}, year={2014}, url={https://reference.wolfram.com/language/ref/Ball.html}, note=[Accessed: 21-November-2024 ]}