BellB
背景
- BellB 是一个返回贝尔数或多项式的数学函数. 尤其是,BellB[n,x] 返回第
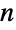
 个贝尔多项式
个贝尔多项式 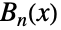 ,BellB[n] 返回第
,BellB[n] 返回第 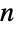
 个贝尔数
个贝尔数 ![TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2] TemplateBox[{n}, BellB]=TemplateBox[{n, 1}, BellB2]](Files/BellB.zh/10.png) . 贝尔多项式可以根据指数生成函数
. 贝尔多项式可以根据指数生成函数 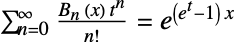 确定. 贝尔数也满足递归关系
确定. 贝尔数也满足递归关系 ![B_(n+1)=sum_(k=0)^nTemplateBox[{n, k}, Binomial]B_k B_(n+1)=sum_(k=0)^nTemplateBox[{n, k}, Binomial]B_k](Files/BellB.zh/12.png) . 前几个贝尔多项式
. 前几个贝尔多项式 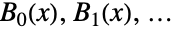 是
是 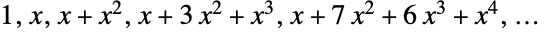 ,其中前几个贝尔数
,其中前几个贝尔数 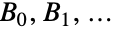 是
是 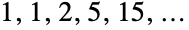 .
. - 贝尔多项式也称之为指数多项式或更确切“完整指数贝尔多项式”,有时表示为
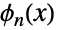 . 贝尔多项式是根据数学家和数学诠释者 Eric Temple Bell 命名的,他在 1934 年写的.
. 贝尔多项式是根据数学家和数学诠释者 Eric Temple Bell 命名的,他在 1934 年写的. - 多项式
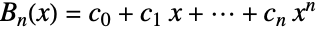 的诠释是如果有
的诠释是如果有 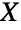 的
的 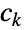 分区成
分区成 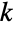 部分,那么
部分,那么 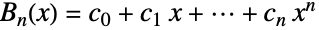 . 而且,如果有
. 而且,如果有 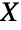 的
的 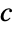 个全部分区,那么
个全部分区,那么 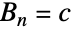 . 例如,假定
. 例如,假定 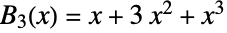 ,集合
,集合 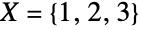 有
有 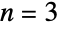 个元素可以分成
个元素可以分成 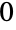 个部分和
个部分和 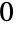 种形式
种形式 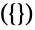 ;
;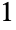 个部分和
个部分和 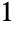 种形式 (
种形式 (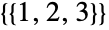 );
);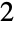 个部分和
个部分和 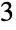 种形式 (
种形式 (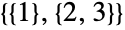 、
、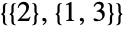 和
和 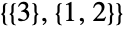 ) 以及
) 以及 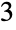 个部分和
个部分和 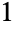 种形式 (
种形式 (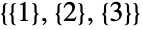 ). 因为有 5 种形式分区
). 因为有 5 种形式分区 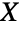 ,所以
,所以 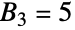 .
. - 贝尔多项式和贝尔数是 BellY 函数的特殊形式,其中
![TemplateBox[{n, x}, BellB2]=sum_(k=0)^nY_(n,k)(x,...,x) TemplateBox[{n, x}, BellB2]=sum_(k=0)^nY_(n,k)(x,...,x)](Files/BellB.zh/45.png) 且
且 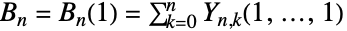 . 让
. 让 ![TemplateBox[{n, k}, StirlingS2] TemplateBox[{n, k}, StirlingS2]](Files/BellB.zh/47.png) 表示第二种的 Stirling 数,由 StirlingS2、
表示第二种的 Stirling 数,由 StirlingS2、![B_n=B_n(1)=sum_(k=0)^nTemplateBox[{n, k}, StirlingS2] B_n=B_n(1)=sum_(k=0)^nTemplateBox[{n, k}, StirlingS2]](Files/BellB.zh/48.png) 返回.
返回.
范例
打开所有单元关闭所有单元范围 (5)
应用 (4)
属性和关系 (7)
BellB 的指数母函数:
PoissonDistribution 的 ![]()
![]() 矩量由
矩量由 ![]()
![]() 贝尔多项式在它的均值
贝尔多项式在它的均值 ![]() 中给出:
中给出:
用 FullSimplify 化简包含 BellB 的表达式:
使用 IntegerPartitions 对满足指标约束的项直接求和:
与 BellB 的结果比较:
FindSequenceFunction 可以识别 BellB 序列:
可能存在的问题 (1)
BellB 的第一个自变量必须是一个非负值整数:
Wolfram Research (2007),BellB,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BellB.html.
文本
Wolfram Research (2007),BellB,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BellB.html.
CMS
Wolfram 语言. 2007. "BellB." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BellB.html.
APA
Wolfram 语言. (2007). BellB. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BellB.html 年