BesselI[n,z]
第1種変形ベッセル(Bessel)関数 ![]() を与える.
を与える.




BesselI
BesselI[n,z]
第1種変形ベッセル(Bessel)関数 ![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
![TemplateBox[{n, z}, BesselI] TemplateBox[{n, z}, BesselI]](Files/BesselI.ja/2.png) は,微分方程式
は,微分方程式 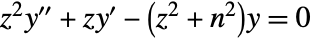 を満足させる.
を満足させる.- BesselI[n,z]は,複素 z 平面上,
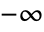 〜
〜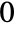 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ. - FullSimplifyとFunctionExpandはBesselIの変換規則を含む.
- 特別な引数の場合,BesselIは,自動的に厳密値を計算する.
- BesselIは任意の数値精度で評価できる.
- BesselIは自動的にリストに縫い込まれる.
- BesselIはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開く すべて閉じる例 (5)
スコープ (50)
数値評価 (6)
BesselIを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のBesselI関数を計算することもできる:
特定の値 (4)
可視化 (4)
関数の特性 (12)
整数 ![]() について,
について,![]() は
は ![]() が偶数か奇数かによって,
が偶数か奇数かによって,![]() について偶関数か奇関数かである:
について偶関数か奇関数かである:
BesselIは n の奇数値について非減少である:
![]() は,
は,![]() が非整数のときは,
が非整数のときは,![]() (
(![]() を含む可能性あり)のとき特異である:
を含む可能性あり)のとき特異である:
BesselIは n の偶数値について凸である:
TraditionalFormによる表示:
積分 (4)
級数展開 (6)
積分変換 (3)
関数の恒等式と簡約 (3)
アプリケーション (2)
半径r,長さaで単位長あたりの固定数の回転があるソルノイドのインダクタンス:
ガウスの非相対論的極限を持つ相対論的3D非マルコフ推移確率分布関数:
上記の正規化 ![]() はBesselIに含まれる変数の変更
はBesselIに含まれる変数の変更 ![]() の後で計算される:
の後で計算される:
特性と関係 (4)
関連するガイド
-
▪
- ベッセル(Bessel)関連関数 ▪
- 特殊関数 ▪
- 連分数と有理近似
履歴
1988 で導入 (1.0) | 1999 で更新 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2) ▪ 2021 (13.0) ▪ 2022 (13.1)
テキスト
Wolfram Research (1988), BesselI, Wolfram言語関数, https://reference.wolfram.com/language/ref/BesselI.html (2022年に更新).
CMS
Wolfram Language. 1988. "BesselI." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/BesselI.html.
APA
Wolfram Language. (1988). BesselI. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BesselI.html
BibTeX
@misc{reference.wolfram_2025_besseli, author="Wolfram Research", title="{BesselI}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/BesselI.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_besseli, organization={Wolfram Research}, title={BesselI}, year={2022}, url={https://reference.wolfram.com/language/ref/BesselI.html}, note=[Accessed: 17-February-2026]}