CategoricalDistribution

CategoricalDistribution[{c1,c2,…}]

クラス c1，c2等で一様カテゴリ分布を表す．

CategoricalDistribution[{c1,c2,…},{w1,w2,…}]

クラス ciで重みが wiのカテゴリ分布を表す．

CategoricalDistribution[{{a1,a2,…},{b1,b2,…},…}]

領域 {a1,a2,…}×{b1,b2,…}×…上で多変量一様カテゴリ分布を表す．

CategoricalDistribution[domain,weights]

配列の weights を使って領域の各要素の確率を定義する．

詳細とオプション

  • カテゴリ分布は，その領域が非順序クラス（例："A"，"B"，"C"）からなる離散分布で，ものの有限集合の確率測度を与えるためによく使われる．
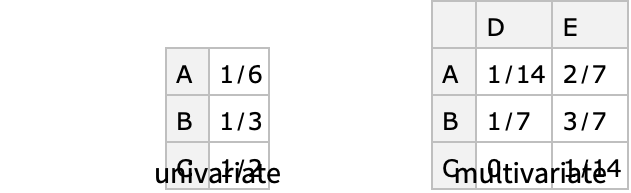
  • カテゴリ分布は1つあるいは複数の変数を持つことができる．各領域要素についての確率は分割表で可視化できる．
  • CategoricalDistribution[…]は，RandomVariate，PDF，Probability，Expectation等の関数で使うことができる．
  • CategoricalDistributionは非数値的分布で，MeanやCDF等の関数と一緒に使うことはできない．
  • CategoricalDistribution[domain,weights]の配列次元の weights は domain で定義された各変数のクラス数と一致しなければならない．
  • 配列の weights はSparseArray[…]形式で与えることができる．
  • 重みは，定義されると確率になるように正規化される．
  • CategoricalDistribution[{c1w1,c2w2,…}]を使ってクラス ciと重み wiを定義することができる．
  • CategoricalDistribution[{{c11,c12,…}w1,elem2w2,…}]を使って多変量領域の要素 elemi（クラスのリスト）とその重み wiが定義できる．省略された要素にはデフォルトで重み0が与えられる．
  • CategoricalDistribution[{elem1w1,elem2w2,…, _val}]における欠略された要素には重み val が与えられる．
  • CategoricalDistribution[domain,{elem1w1,elem2w2,…}]を使って分布領域といくつかの分布要素の確率の両方が指定できる．
  • Information[CategoricalDistribution[…]]は分布についてのレポートを与える．
  • CategoricalDistributionについてのInformationには以下の特性が含まれる．
  • "Categories"分布クラスのリスト
    "Dimension"変数の数
    "DomainElements"領域内の全要素
    "DomainSize"領域内の要素数
    "Entropy"厳密なエントロピー
    "NEntropy"近似エントロピー
    "Probabilities"確率の連想
    "ProbabilityArray"確率配列
    "ProbabilityPlot"確率関数の可視化
    "ProbabilityTable"Datasetにおける確率
    "Properties"使用可能な全特性
    "TopProbabilities"最高確率の要素のリスト
    "TopProbabilities"n確率が高いものから n 個の要素

例題

すべて開くすべて閉じる

例  (2)

一変量で一様なカテゴリ分布を作る：

この分布からランダムなサンプルを生成する：

クラスの確率質量を計算する：

重み付きの一変量カテゴリ分布を作成する：

分布からランダムなサンプルを生成する：

クラスの確率質量を計算する：

確率をプロットで可視化する：

スコープ  (15)

一変量の定義  (4)

シンボルがクラスの一変量カテゴリ分布を定義する：

この分布からサンプルを生成する：

規則を使って一変量カテゴリ分布を定義する：

分布の情報を可視化する：

領域と規則を使って一変量カテゴリ分布を定義する：

分布についての情報を可視化する：

未定義要素のデフォルトの重みを指定する：

分布についての情報を可視化する：

繰返し要素でカテゴリ分布を定義する：

確率は繰返し要素の数に比例する：

多変量の定義  (4)

多変量のカテゴリ分布を作成する：

分布からランダムなサンプルを生成する：

要素の確率質量を計算する：

分布の分割表を可視化する：

周辺分布を第1変数について計算する：

周辺分布の分割表を可視化する：

疎な配列を使って多変量カテゴリ分布を定義する：

その確率表を可視化する：

領域と規則を定義することで多変量カテゴリ分布を定義する：

その確率表を可視化する：

未定義の要素が与えられた重みを持つように指定する：

確率表を可視化する：

たくさんの変数を持つカテゴリ分布を作成する：

その確率表を可視化する：

情報  (2)

一変量分布を作成する：

この分布についての情報のレポートを取得する：

使用可能な情報特性のリストを得る：

クラスのリストを得る：

全クラスの確率を得る：

確率を可視化する：

分布の厳密なエントロピーを得る：

多変量分布を作成する：

この分布についての情報のレポートを得る：

使用可能な情報特性のリストを得る：

各変数についての可能なクラスを得る：

使用可能な全領域要素を得る：

すべての領域要素についての確率を得る：

最高確率の要素を2つ得る：

確率を可視化する：

この分布の厳密なエントロピーを得る：

記号による重み  (2)

記号（非数値）パラメータでカテゴリ分布を定義する：

確率表を可視化する：

パラメータ a を数値で置換する：

確率表を可視化する：

記号パラメータでカテゴリ分布を定義する：

RandomVariateは評価されない：

記号パラメータを数値で置換する：

領域外の動作  (1)

カテゴリ分布を定義する：

「領域外」クラスの確率質量は定義されていないので，PDFは評価されない：

領域外のクラスを領域クラスで置換する：

確率と推定  (2)

多変量分布を作成する：

第1変数が"A"である確率を計算する：

MarginalDistributionで計算された同じ確率と比較する：

多変量分布を作成する：

Expectationを使ってそのエントロピーを計算する：

Informationで与えられるようなエントロピーと比較する：

NExpectationを使ってエントロピーを計算する：

"MonteCarlo"メソッドを使うように指定する：

使用するサンプル数を指定する：

アプリケーション  (2)

分類器を訓練する：

与えられた入力に対して予測された分布を返す：

予測された分布からランダムなサンプルを生成する：

タイタニック号の乗客のデータ集合をロードする：

3つのカテゴリ変数を抽出し，それらを合わせた出現回数を数える：

これらの回数からカテゴリ分布を作成する：

この分布の確率表を可視化する：

乗客の生存確率を計算する：

女性の乗客の生存確率を計算する：

特性と関係  (1)

カテゴリ分布を作成する：

領域の各要素についての確率を得る：

確率が負になることはない：

確率を合計すると常に1になる：

Wolfram Research (2020), CategoricalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

テキスト

Wolfram Research (2020), CategoricalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

CMS

Wolfram Language. 2020. "CategoricalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

APA

Wolfram Language. (2020). CategoricalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CategoricalDistribution.html

BibTeX

@misc{reference.wolfram_2024_categoricaldistribution, author="Wolfram Research", title="{CategoricalDistribution}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CategoricalDistribution.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_categoricaldistribution, organization={Wolfram Research}, title={CategoricalDistribution}, year={2020}, url={https://reference.wolfram.com/language/ref/CategoricalDistribution.html}, note=[Accessed: 17-November-2024 ]}