CategoricalDistribution

CategoricalDistribution[{c1,c2,…}]

在 c1、c2 等类别上表现均匀范畴分布.

CategoricalDistribution[{c1,c2,…},{w1,w2,…}]

在权重为 wi 的类别 ci 上表现范畴分布.

CategoricalDistribution[{{a1,a2,…},{b1,b2,…},…}]

在域 {a1,a2,…}×{b1,b2,…}×… 上表现多变量均匀范畴分布.

CategoricalDistribution[domain,weights]

用数组 weights 定义域中每个元素的概率.

更多信息和选项

  • 范畴分布是一个离散分布，它的域由无序类别（如："A"、"B"、"C"）组成，通常用于对事物的有限集合进行概率测度.
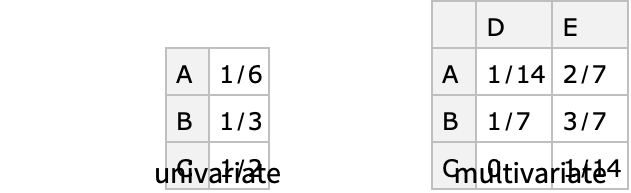
  • 范畴分布可以有一个或多个变量. 列联表显示了域中每个元素的概率：
  • CategoricalDistribution[…] 可用于诸如 RandomVariate、PDF、Probability 和 Expectation 之类的函数中.
  • CategoricalDistribution[…] 不是数字分布：不能对其使用诸如 Mean 或 CDF 之类的函数.
  • 在 CategoricalDistribution[domain,weights] 中，数组 weights 的维度必须与 domain 中定义的每个变量的类别数匹配.
  • 可用 SparseArray[…] 形式给出数组 weights.
  • 定义了权重的情况下，权重将被规范化为概率.
  • CategoricalDistribution[{c1w1,c2w2,…}] 可用于定义类别 ci 和权重 wi.
  • CategoricalDistribution[{{c11,c12,…}w1,elem2w2,…}] 可用于定义多元域元素 elemi（类的列表）及其权重 wi. 省略的元素默认权重为 0.
  • 在 CategoricalDistribution[{elem1w1,elem2w2,…, _val}] 中，省略元素的权重为 val.
  • CategoricalDistribution[domain,{elem1w1,elem2w2,…}] 可用于指定分布域和域中某些元素的概率.
  • Information[CategoricalDistribution[…]] 给出有关该分布的报告.
  • CategoricalDistribution 的 Information 包括以下属性：
  • "Categories"分布类别列表
    "Dimension"变量的个数
    "DomainElements"域中的所有元素
    "DomainSize"域中元素的个数
    "Entropy"精确熵
    "NEntropy"近似熵
    "Probabilities"概率关联
    "ProbabilityArray"概率数组
    "ProbabilityPlot"概率函数可视化
    "ProbabilityTable"Dataset 中的概率
    "Properties"所有可用属性
    "TopProbabilities"概率最高的元素的列表
    "TopProbabilities"n概率最高的 n 个元素

范例

打开所有单元关闭所有单元

基本范例  (2)

创建一个单变量均匀范畴分布：

根据分布生成随机样本：

计算一个类别的概率质量：

创建加权单变量范畴分布：

根据分布生成随机样本：

计算类别的概率质量：

可视化概率：

范围  (15)

单变量定义  (4)

定义一个以符号表示类别的单变量范畴分布：

根据分布生成样本：

用规则定义单变量范畴分布：

可视化分布的信息：

用域和规则定义单变量范畴分布：

可视化分布的信息：

指定未定义元素的默认权重：

可视化分布的信息：

定义包含重复元素的范畴分布：

概率与重复元素的数量成正比：

多变量定义  (4)

创建多变量范畴分布：

根据分布生成随机样本：

计算一个元素的概率质量：

可视化分布的列联表：

计算第一个变量的边际分布：

可视化边际分布的列联表：

用稀疏数组定义多变量范畴分布：

可视化概率表：

通过定义域和规则来定义多变量范畴分布：

可视化概率表：

指定未定义的元素应具有给定的权重：

可视化概率表：

创建具有许多变量的范畴分布：

可视化概率表：

信息  (2)

创建单变量分布：

获取分布的信息报告：

获取可能的信息属性列表：

获取类别列表：

获取所有类别的概率：

可视化概率：

获取分布的精确熵：

创建多变量分布：

获取分布的信息报告：

获取可能的信息属性列表：

获取每个变量的可能的类别：

获取所有可能的域元素：

获得所有域元素的概率：

获得两个概率最高的元素：

可视化概率：

获取分布的精确熵：

符号权重  (2)

用符号（非数字）参数定义范畴分布：

可视化概率表：

用数字替换参数 a：

可视化概率表：

用符号参数定义范畴分布：

RandomVariate 不进行计算：

用数值替换符号参数：

域外行为  (1)

定义一个范畴分布：

没有定义 "out-of-domain" 类别的概率质量，因此 PDF 不进行计算：

用域内类别替换域外类别：

概率和期望  (2)

创建多变量分布：

计算第一个变量为 "A" 的概率：

与使用 MarginalDistribution 计算相同概率所得到的结果进行比较：

创建多变量分布：

用 Expectation 计算熵：

与 Information 给出的熵相比较：

用 NExpectation 计算熵：

指定使用 "MonteCarlo" 方法：

指定应使用的样本数：

应用  (2)

训练一个分类器：

返回给定输入的预测分布：

根据预测的分布生成随机样本：

加载泰坦尼克号上乘客的数据集：

提取三个类别变量，并计算它们的组合出现的次数：

根据这些计数创建范畴分布：

可视化分布的概率表：

计算乘客幸存的可能性：

计算女性乘客幸存的可能性：

属性和关系  (1)

创建一个范畴分布：

获取域中每个元素的概率：

概率永远不会为负：

概率的总和总是为一：

Wolfram Research (2020)，CategoricalDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

文本

Wolfram Research (2020)，CategoricalDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

CMS

Wolfram 语言. 2020. "CategoricalDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CategoricalDistribution.html.

APA

Wolfram 语言. (2020). CategoricalDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CategoricalDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_categoricaldistribution, author="Wolfram Research", title="{CategoricalDistribution}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CategoricalDistribution.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_categoricaldistribution, organization={Wolfram Research}, title={CategoricalDistribution}, year={2020}, url={https://reference.wolfram.com/language/ref/CategoricalDistribution.html}, note=[Accessed: 17-November-2024 ]}