CauchyMatrix

CauchyMatrix[x,y]

表示由生成向量 x 和 y 作为结构化数组给出的柯西矩阵.

CauchyMatrix[x]

等价于 CauchyMatrix[x,x].

CauchyMatrix[cmat]

将柯西矩阵 cmat 转换为结构化数组.

更多信息和选项

  • 当表示为结构化数组时，柯西矩阵可进行更高效的存储和更高效的运算，包括 Det、Inverse 和 LinearSolve.
  • 柯西矩阵出现在与有理插值、保形映射、n-体仿真和奇异核积分方程离散化相关的计算中.
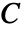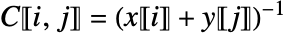  • 给定生成向量 x 和 y，所得的柯西矩阵 中的元素由 给出.
  • CauchyMatrix 可以加快运算速度的计算包括：
  • Det用时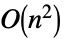
    Inverse用时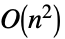
    LinearSolve用时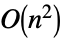
  • 对于 CauchyMatrix sa，可通过 sa["prop"] 访问以下属性 "prop"：
  • "XVector"生成向量 x
    "YVector"生成向量 y
    "Properties"支持的属性的列表
    "Structure"结构化数组的类型
    "StructuredData"结构化数组存储的内部数据
    "StructuredAlgorithms"可对结构化数组使用特殊方法的函数的列表
    "Summary"汇总信息，用 Dataset 表示
  • Normal[CauchyMatrix[x]] 以普通矩阵的方式给出柯西矩阵.
  • CauchyMatrix[…,TargetStructure->struct] 以 struct 指定的格式返回柯西矩阵. 可能的设置包括：
  • Automatic自动选择返回的表示
    "Dense"以稠密矩阵的形式表示矩阵
    "Structured"以结构化数组的形式表示矩阵
    "Symmetric"将矩阵表示为对称矩阵
  • CauchyMatrix[…,TargetStructureAutomatic] 等价于 CauchyMatrix[…,TargetStructure"Structured"].

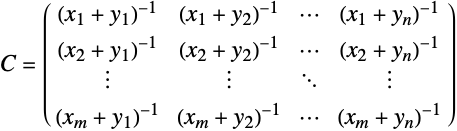
范例

打开所有单元关闭所有单元

基本范例  (2)

构建柯西矩阵：

显示元素：

Normal 可将 CauchyMatrix 转换成普通形式的矩阵：

构建含有符号元素的柯西矩阵：

显示元素：

获取行列式：

范围  (6)

生成一个对称的柯西矩阵：

显示元素：

获取普通形式的矩阵：

生成矩形柯西矩阵：

显示元素：

显示元素：

以结构化数组的形式表示稠密柯西矩阵：

显示元素：

结构化表示通常使用更少的内存：

CauchyMatrix 对象含有可给出有关数组信息的属性：

"XVector" 和 "YVector" 属性给出了柯西矩阵的生成向量：

"Summary" 属性给出了有关数组的信息的简明摘要：

"StructuredAlgorithms" 属性列出了含有结构化算法的函数：

合适的情况下，结构化算法会返回另一个 CauchyMatrix 对象：

转置也是一个 CauchyMatrix：

柯西矩阵及其转置的乘积不再是柯西矩阵：

选项  (1)

TargetStructure  (1)

以稠密矩阵的形式返回柯西矩阵：

以结构化数组的形式返回柯西矩阵：

将柯西矩阵返回为对称矩阵：

应用  (3)

将 Hilbert 矩阵表示为 CauchyMatrix：

与 HilbertMatrix 比较：

用数值法计算大型希尔伯特矩阵的逆：

用结构化版本得到结果更准确：

用 CauchyMatrix 计算具有固定极点的插值有理函数的系数：

构建有理函数：

可视化复平面中的插值：

检查有理插值是否经过所有给定点：

用 CauchyMatrix 定义 Parter 矩阵：

Parter 矩阵既是 Cauchy 矩阵，也是 Toeplitz 矩阵：

Parter matrix 矩阵的主奇异值聚集在 周围：

属性和关系  (2)

将柯西矩阵表示为对角矩阵、范德蒙矩阵及其逆矩阵的乘积：

将柯西矩阵表示为对角矩阵、范德蒙德矩阵和汉克尔矩阵的乘积：

可能存在的问题  (3)

文献有时使用柯西矩阵的不同定义，其中第二个生成向量被取负：

如果任一生成向量含有重复元素，则无法构建柯西矩阵：

如果任一生成向量的分量是另一个生成向量的分量的负值，则无法构建柯西矩阵：

Wolfram Research (2022)，CauchyMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CauchyMatrix.html （更新于 2024 年）.

文本

Wolfram Research (2022)，CauchyMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CauchyMatrix.html （更新于 2024 年）.

CMS

Wolfram 语言. 2022. "CauchyMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/CauchyMatrix.html.

APA

Wolfram 语言. (2022). CauchyMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CauchyMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_cauchymatrix, author="Wolfram Research", title="{CauchyMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CauchyMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cauchymatrix, organization={Wolfram Research}, title={CauchyMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/CauchyMatrix.html}, note=[Accessed: 21-November-2024 ]}