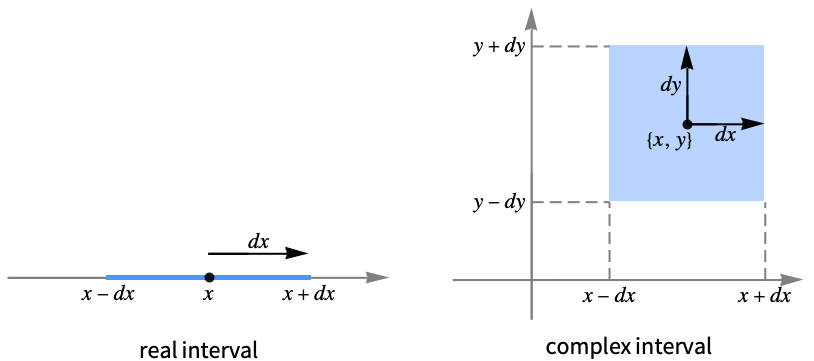
CenteredInterval[x,dx]
実数 x および dx に対して実数区間![]() を含む中心がある区間を与える.
を含む中心がある区間を与える.
CenteredInterval[x+ y,dx+ dy]
複素長方形![]() を含む中心がある区間を与える.
を含む中心がある区間を与える.
近似数 c に対して c の誤差境界内のすべての値を含む中心がある区間を与える.


CenteredInterval
CenteredInterval[x,dx]
実数 x および dx に対して実数区間![]() を含む中心がある区間を与える.
を含む中心がある区間を与える.
CenteredInterval[x+ y,dx+ dy]
複素長方形![]() を含む中心がある区間を与える.
を含む中心がある区間を与える.
近似数 c に対して c の誤差境界内のすべての値を含む中心がある区間を与える.
詳細


- 中心がある区間は中心半径区間あるいは中半径区間としても知られている.
- CenteredIntervalは,通常,数値計算で累積された誤差の検証済み境界を得るために使われる.中心がある区間の計算は,関数の全引数の誤差境界が与えられると関数値の誤差の信頼できる境界を与える.
- CenteredInterval[…]は中心がある区間オブジェクトΔを,中心
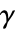 ,半径
,半径 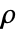 で与える.
で与える.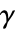 と
と 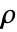 は2つの分母をベキ乗したガウスの有理数である.
は2つの分母をベキ乗したガウスの有理数である.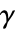 と
と 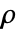 が実数ならΔは実区間
が実数ならΔは実区間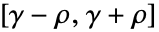 を表し,それ以外の場合はΔは複素長方形
を表し,それ以外の場合はΔは複素長方形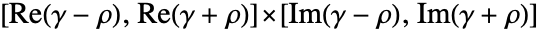 を表す.
を表す. - 中心がある区間引数は算術演算および多くの数学関数で使うことができる.f[Δ1,…,Δn]は中心がある区間オブジェクトΔを与える.これには任意の ai∈Δiについての f[a1,…,an]が含まれる.
- IntervalMemberQは区間への帰属や区間間の包含関係の決定に使うことができる.
- EqualやLess等の有理演算子は,互いに素な区間を与えられると常に明示的なTrueまたはFalseの結果を与える.
- StandardFormおよび関連する形式では,CenteredIntervalオブジェクトは中心と半径の近似値しか表示されない省略形で出力される.
- NormalはCenteredIntervalオブジェクトを確度が半径に対応する任意精度数に変換する.
- Information[CenteredInterval[…], prop]は中心半径区間の特性 prop を与える.以下は指定可能な特性である.
-
"Center" 区間の中心 "Radius" 区間の半径 "Bounds" 区間内の値の境界 - Det,Inverse,LinearSolve,Eigensystem等の線形代数の演算は,CenteredInterval成分を持つ行列に使うことができる.
例題
すべて開く すべて閉じる例 (3)
スコープ (27)
中心・半径区間を構築する (7)
有界のIntervalオブジェクトを中心がある区間に変換する:
非零の機械精度数は$MachinePrecision精度数として扱われる:
区間演算 (5)
値の集合が非有界のときは,区間演算操作はIndeterminateを返す:
区間特性 (5)
IntervalIntersectionを使って交点を計算する:
空区間はInterval[]として表される:
線形代数 (10)
CenteredInterval行列の積:
m と n のランダムな代表の mrep と nrep を求める:
mn が mrep と nrep の積を含むことを確認する:
CenteredInterval行列を整数乗する:
mpow がMatrixPower[mrep,17]を含むことを確認する:
CenteredInterval行列の指数行列:
CenteredInterval行列の行列式:
CenteredInterval行列の逆行列:
CenteredInterval行列について ![]() を解く:
を解く:
m と b のランダムな代表の mrep と brep を求める:
sol がLinearSolve[mrep,brep]を含むことを確認する:
CenteredInterval行列の固有系:
ベクトルを並べ替えてスケーリングし直した後で,vals が rvals,vecs が rvecs を含むことを確認する:
CenteredInterval行列のLU分解:
実対称正定値CenteredInterval行列のコレスキー(Cholesky)分解:
CenteredInterval行列の固有多項式:
特性と関係 (2)
Intervalは端点を指定することで与えられた実区間を表す:
区間をCenteredInterval表現に変換する:
考えられる問題 (1)
テキスト
Wolfram Research (2021), CenteredInterval, Wolfram言語関数, https://reference.wolfram.com/language/ref/CenteredInterval.html.
CMS
Wolfram Language. 2021. "CenteredInterval." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CenteredInterval.html.
APA
Wolfram Language. (2021). CenteredInterval. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CenteredInterval.html
BibTeX
@misc{reference.wolfram_2025_centeredinterval, author="Wolfram Research", title="{CenteredInterval}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/CenteredInterval.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_centeredinterval, organization={Wolfram Research}, title={CenteredInterval}, year={2021}, url={https://reference.wolfram.com/language/ref/CenteredInterval.html}, note=[Accessed: 06-February-2026]}