Covariance
Covariance[v,w]
给出向量 v 和 w 的协方差.
Covariance[a,b]
给出了矩阵 a 和 b 的交叉协方差矩阵.
Covariance[a]
给出了矩阵 a 中观测值的自协方差矩阵.
Covariance[dist]
给出多元符号分布的自协方差矩阵 dist.
Covariance[dist,i,j]
给出多变量符号分布 dist 的第 (i,j) 个协方差.
更多信息


- Covariance 通常用于测量协变,即一个变量是否与另一个变量有相似的变化趋势.
- Covariance[v,w] 给出了 v 和 w 之间协方差
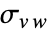 的无偏估计值.
的无偏估计值. - 对于长度为
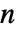 的向量
的向量 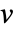 和
和 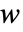 ,协方差估值 Covariance[v,w] 由
,协方差估值 Covariance[v,w] 由 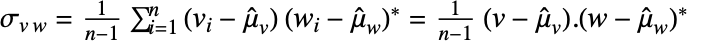 给出,其中
给出,其中 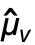 =Mean[v].
=Mean[v]. - 对于维度分别为
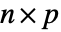 和
和 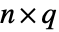 且列索引分别为
且列索引分别为 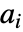 和
和 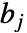 的矩阵
的矩阵 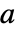 和
和 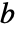 ,Covariance[a,b] 是一个
,Covariance[a,b] 是一个 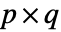 矩阵,其元素由
矩阵,其元素由 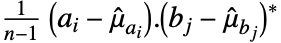 给出:
给出: - 其中
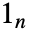 是 1 的
是 1 的 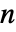 -向量,
-向量,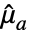 是 Mean[a] 且
是 Mean[a] 且 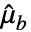 是 Mean[b].
是 Mean[b]. - 对于一个有
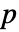 列的矩阵 a,Covariance[a] 是一个由 Covariance[a, a] 给出的
列的矩阵 a,Covariance[a] 是一个由 Covariance[a, a] 给出的 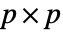 矩阵.
矩阵. - Covariance 适用于任何 VectorQ 向量或 MatrixQ 矩阵.
- Covariance[dist,i,j] 给出 Expectation[(xi-μi)(xj-μj),{x1,x2,…}∈dist],其中 μi 是 dist 平均值的第 i
 个分量. »
个分量. » - Covariance[dist] 给出一个协方差矩阵,其第 (i,j)
 个项由 Covariance[dist,i,j] 给出. »
个项由 Covariance[dist,i,j] 给出. »
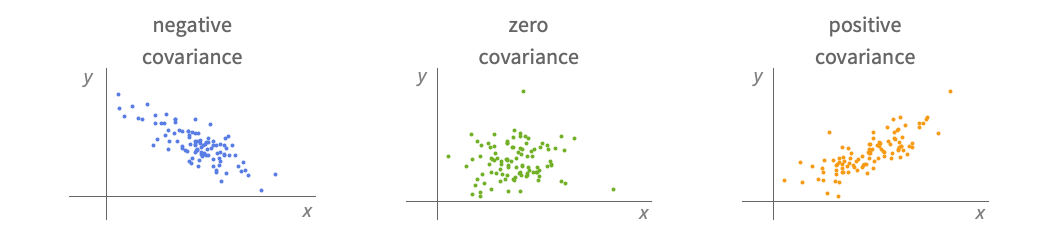
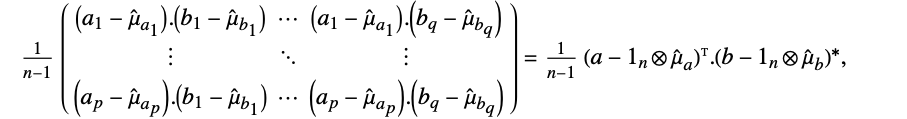
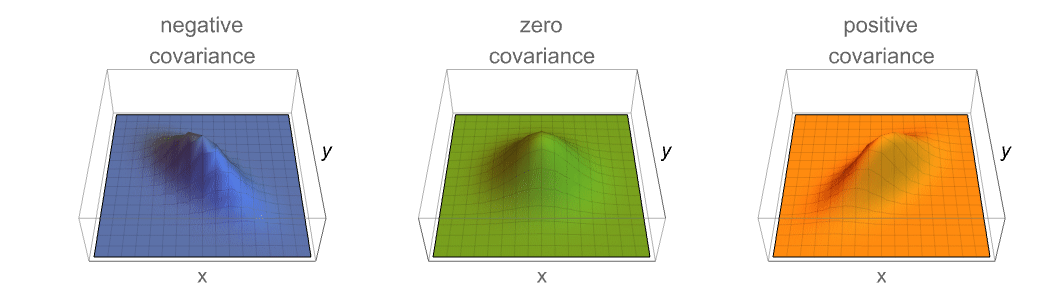
范例
打开所有单元关闭所有单元范围 (13)
数据 (8)
分布和过程 (5)
TemporalData 在时刻 ![]() 和
和 ![]() 的协方差矩阵:
的协方差矩阵:
应用 (3)
属性和关系 (9)
对于均值为零的分布,Covariance 和 AbsoluteCorrelation 相同:
SpearmanRho 与应用于秩的 Covariance 相关:
对于过程而言,CovarianceFunction 是协方差矩阵的非对角线项:
对于标准化向量,Covariance 和 Correlation 相同:
文本
Wolfram Research (2007),Covariance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Covariance.html (更新于 2024 年).
CMS
Wolfram 语言. 2007. "Covariance." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Covariance.html.
APA
Wolfram 语言. (2007). Covariance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Covariance.html 年