CoxModelFit[{e1,…,en}]
构建基准风险 ![]() 在事件时刻 ei 的模型.
在事件时刻 ei 的模型.
CoxModelFit[{{{ξ11,…,ξ1p},…,{ξn1,…,ξnp}},{e1,…,en}},{f1,…,fm},{x1,…,xp}]
构建形如 ![]() 的 Cox 模型, 其中 fi 取决于xk.
的 Cox 模型, 其中 fi 取决于xk.




CoxModelFit
CoxModelFit[{e1,…,en}]
构建基准风险 ![]() 在事件时刻 ei 的模型.
在事件时刻 ei 的模型.
CoxModelFit[{{{ξ11,…,ξ1p},…,{ξn1,…,ξnp}},{e1,…,en}},{f1,…,fm},{x1,…,xp}]
构建形如 ![]() 的 Cox 模型, 其中 fi 取决于xk.
的 Cox 模型, 其中 fi 取决于xk.
更多信息和选项







- CoxModelFit 用于生存性、可靠性和持续时间分析. 它量化相对生存风险,并估计底层的基准风险.
- CoxModelFit 返回符号式 CoxModel 对象,以表示它构建的比例风险模型. 模型的属性和诊断量可以从 model["property"] 获得.
- 可用的模型属性列表可以通过使用 model["Properties"] 获得.
- 事件 ei 的形式服从 EventData 中所用的形式.
- CoxModelFit 生成条件风险函数
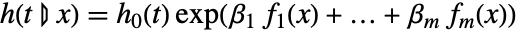 ,与基准风险函数
,与基准风险函数 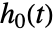 成一定比例.
成一定比例. - 模型是半参数式,参数
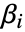 可通过部分似然最大化求得. 基准风险
可通过部分似然最大化求得. 基准风险  利用非参数方法估计得到.
利用非参数方法估计得到. - 仅估计
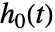 的零模型可利用 CoxModelFit[e] 指定,它等价于 CoxModelFit[{ξ,e},{},{x1,…,xp}].
的零模型可利用 CoxModelFit[e] 指定,它等价于 CoxModelFit[{ξ,e},{},{x1,…,xp}]. - 在基函数 fi 中指定的常数值在拟合中被忽略,并在基准风险
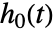 的估计中被吸收.
的估计中被吸收. - 下列属性表与模型参数分量
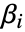 的估计、诊断和检验相关. »
的估计、诊断和检验相关. » - 与 model["property"] 所用的数据和所得到的拟合函数相关的属性包括:
-
"BaselineList" 包含各层基准协变量水平的列表 "BasisFunctions" 基函数 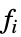 的列表
的列表"BestFitParameters" 参数估计量 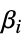
"Data" 协变量输入数据的矩阵 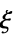
"EventData" 事件输入数据 
"RelativeRisk" 模型参数的相对风险 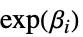
"StrataModels" 包含各层子模型的列表 "StrataSummary" 包含各层名称和计数配对的列表 - 测量拟合优度的属性包括:
-
"AIC" 赤池信息量准则 "BIC" 施瓦兹贝叶斯信息准则 "LogLikelihood" 模拟对数似然 "MaxRSquared" 可能的 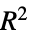 系数的最大值
系数的最大值"RSquared" 伪决定系数 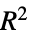
- 残差和影响力的测量类型:
-
"BetaDifferences" 对参数值影响的 DFBETA 测量方法 "CoxSnellResiduals" Cox–Snell 类型残差 "DevianceResiduals" 按比例调整的鞅残差 "MartingaleResiduals" 随时间的推移事件的超出数目估计 "ScaledBetaDifferences" 利用模型标准差计算的 DFBETA "SchoenfeldResiduals" 舍恩菲尔德型残差 "ScoreResiduals" Score 残差 - 参数估计的属性和诊断包括:
-
"CovarianceMatrix" 模型参数的协方差估计 "InformationMatrix" 模型参数的信息矩阵 "LikelihoodRatioStatistic" 拟合模型与零模型的似然比 "ParameterConfidenceIntervals" 参数估计的置信区间 "ParameterStandardErrors" 模型参数的标准误差 "ParameterTable" 拟合参数信息表 "ParameterTableEntries" 参数表中的条目 "RelativeRiskConfidenceIntervals" 相对风险估计值的置信区间 "RiskScores" 对每个观察值的风险评分 "ScoreStatistic" 比较拟合模型和零模型的 Score 统计量 "TestTable" 模型参数的显著信息表 "TestTableEntries" 检验表中的条目 "TestTableEntriesFunction" 用检验表函数创建的表格中的条目 "TestTableFunction" 在指定零假设下创建的检验表 "WaldStatistic" 比较拟合模型和零模型的 Wald 统计量 - 正如在 SurvivalModelFit 中一样,获得模型
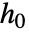 的非参数分量的信息是可能的,包括生存概率的估计量、生存置信区间和矩估计量. »
的非参数分量的信息是可能的,包括生存概率的估计量、生存置信区间和矩估计量. » - CoxModelFit 具有 SurvivalModelFit 中可用的所有属性.
- 与
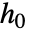 相关的属性的指定与 SurvivalModelFit 中一样,但额外要求协变量水平 x0 以 model["property"][x0] 的形式给出.
相关的属性的指定与 SurvivalModelFit 中一样,但额外要求协变量水平 x0 以 model["property"][x0] 的形式给出. - 通过指定 model[h][x0] 中的形式 h,可以得到协变量水平 x0 时风险率
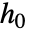 的不同函数形式. 可以使用以下形式.
的不同函数形式. 可以使用以下形式. -
"CDF" 累积分布函数 "CHF" 累积风险函数 "SF" 生存函数 - CoxModelFit 在特定点 t 和协变量水平 x0 时的拟合函数值 h 可从 model[h][x0][t] 得到. model[h][][t] 给出基准风险 h0[t] 的形式 h.
- 指定 Normal[model] 给出 model["SF"][][t] 的纯函数形式.
- CoxModelFit 接受以下选项:
-
ConfidenceLevel 95/100 用于区间和带的水平 ConfidenceRange All 同步置信带的范围 ConfidenceTransform "LogLog" 使用的置信变换 Method Automatic 用于模型拟合的方法 NominalVariables None 视为分类的变量 StrataVariables None 视为层的变量 WorkingPrecision Automatic 内部计算所用的精度 - 当 ConfidenceLevel->p 时,计算用于各种函数形式和参数估计时的概率 p 置信区间和置信带.
- ConfidenceRange->{tmin,tmax} 给出拟合函数在 tmin 和 tmax 之间的概率 p 同步置信区间和置信带.
- ConfidenceTransform 的可能设置包括 "Linear"、"LogLog"、"ArcSinSqrt"、 "Log"、"Logit" 或者纯函数 g.
- 设置 Method->m 指定用于处理同时发生的事件(ties)的方法。可能的设置如下.
-
"Breslow" 使用 Breslow 部分似然 "Efron" 使用 Efron 部分似然 "Exact" 使用精确的边缘似然 - 默认情况下使用 "Breslow" 方法来处理同时发生的事件.
- 其他方法设置可以在范例的选项部分找到. »
范例
打开所有单元 关闭所有单元范围 (26)
模型规范 (4)
使用 EventData 指定右删失或左截断的响应时间:
参数估计和模型诊断 (6)
生存估计和置信度 (8)
计算 SurvivalFunction、CDF 或累积风险函数的估计量:
所估计的 SurvivalFunction,其中协变量水平为 ![]() 和
和 ![]() :
:
在时刻 ![]() 时,所估计的基准 SurvivalFunction、CDF 和累积风险:
时,所估计的基准 SurvivalFunction、CDF 和累积风险:
制作所估计的 SurvivalFunction 的汇总表:
这些是在模型 "EstimationPoints" 计算的 "PointwiseBands":
一组 Hall–Wellner 同步置信区间,其中协变量水平为 ![]() 和
和 ![]() :
:
这些是在模型 "HallWellnerBands" 计算的 "EstimationPoints":
另外,也可使用 "EqualPrecisionIntervals" 度量同步置信度:
选项 (13)
ConfidenceLevel (3)
ConfidenceLevel 的设置也用于汇总表中:
ConfidenceTransform (3)
Method (3)
如果最后一个观察值删失,生存将在该点外被 Indeterminate:
StrataVariables (1)
应用 (5)
耳螨治疗 (1)
喉癌 (3)
对一组由 90 例被确诊为喉癌的男性患者进行观察. 每个病人被归类为处于四个阶段的癌症之一,其中 1 是最不严重的,而 4 是最严重的. 要研究的是是癌症的阶段是否与生存显著关联:
在 5% 水平下,第 2 阶段患者死亡的风险与第 1 阶段相比没有不同:
求与第 2 阶段喉癌患者相比,第 4 阶段患者死亡的相对风险的估计值:
在 5% 水平下,第 4 阶段患者死亡的风险高于第 2 阶段患者:
已知有序层,LogRankTest 可用于进行趋势检验:
属性和关系 (4)
CoxModelFit 是广义的 SurvivalModelFit:
使用 LogRankTest 比较各组的风险率:
相关指南
-
▪
- 生存分析 ▪
- 非参数统计分布 ▪
- 可靠性 ▪
- 用于可靠性分析中的分布 ▪
- 科学数据分析 ▪
- 生命科学和医学:数据与计算 ▪
- 概率和统计 ▪
- 表格建模
文本
Wolfram Research (2012),CoxModelFit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CoxModelFit.html.
CMS
Wolfram 语言. 2012. "CoxModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/CoxModelFit.html.
APA
Wolfram 语言. (2012). CoxModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CoxModelFit.html 年
BibTeX
@misc{reference.wolfram_2025_coxmodelfit, author="Wolfram Research", title="{CoxModelFit}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CoxModelFit.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_coxmodelfit, organization={Wolfram Research}, title={CoxModelFit}, year={2012}, url={https://reference.wolfram.com/language/ref/CoxModelFit.html}, note=[Accessed: 05-February-2026]}