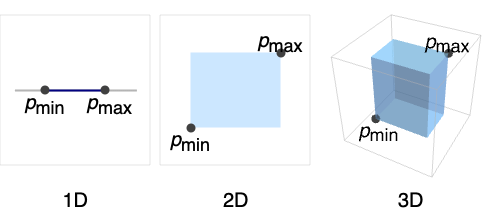
Cuboid
Cuboid[pmin]
represents a unit hypercube with its lower corner at pmin.
Cuboid[pmin,pmax]
represents an axis-aligned filled cuboid with lower corner pmin and upper corner pmax.
Details and Options

- Cuboid is also known as interval, rectangle, square, cube, rectangular parallelepiped, tesseract, hypercube, orthotope, hyperrectangle, and box.
- Cuboid represents the region
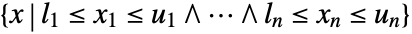 where
where 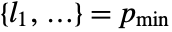 and
and 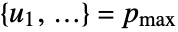 .
. - Cuboid[] is equivalent to Cuboid[{0,0,0}].
- CanonicalizePolyhedron can be used to convert a cuboid to an explicit Polyhedron object.
- Cuboid can be used in Graphics and Graphics3D.
- In graphics, the points pmin and pmax can be Scaled, ImageScaled, Offset, and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, and color.
Examples
open allclose allBasic Examples (5)
Scope (21)
Graphics (11)
Specification (3)
Styling (5)
Regions (10)
Embedding dimension is the dimension of the space in which the cuboid lives:
Geometric dimension is the dimension of the shape itself:
Get conditions for point membership:
The equidistance contours for a cuboid:
Nearest points to an enclosing sphere:
Integrate over a cuboid region:
Applications (8)
Define a cuboid region by length, width, and height:
Total mass for a cuboid region with density given by ![]() :
:
Find the mass of ethanol in a cuboid:
Mass of ethanol in the cuboid:
Create a bounding box from RegionBounds:
Compute the difference in Volume:
Show a sequence of steps in the evolution of a 3D cellular automaton:
Properties & Relations (8)
Use Transpose to convert Cuboid to a range specification:
And conversely, a range specification to a Cuboid specification:
Use Rotate to get all possible cuboids in Graphics3D:
Polygon is a generalization of Cuboid in 2D:
Rectangle is a special case of Cuboid:
Hexahedron is a generalization of Cuboid:
ImplicitRegion can represent any Cuboid:
Parallelepiped can represent any Cuboid:
Cuboid is a norm ball for the ![]() -norm:
-norm:
Text
Wolfram Research (1991), Cuboid, Wolfram Language function, https://reference.wolfram.com/language/ref/Cuboid.html (updated 2019).
CMS
Wolfram Language. 1991. "Cuboid." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Cuboid.html.
APA
Wolfram Language. (1991). Cuboid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Cuboid.html