Cuboid
詳細とオプション

- Cuboidは,区間,長方形,正方形,立方体,四次元直方体,超直方体,超長方形,ボックスとしても知られている.
- Cuboidは領域
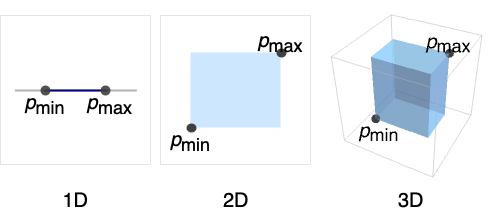
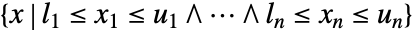 を表す.ただし,
を表す.ただし,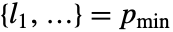 かつ
かつ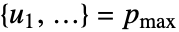 である.
である. - Cuboid[]はCuboid[{0,0,0}]に等しい.
- CanonicalizePolyhedronを使って直方体を明示的なPolyhedronオブジェクトに変換できる.
- CuboidはGraphicsおよびGraphics3Dで使うことができる.
- グラフィックスでは,点 pminおよび pmaxは,Scaled,ImageScaled,Offset,Dynamicの各式でよい.
- グラフィックスの描画は,FaceForm,EdgeForm,Opacity,色等の指示子の影響を受ける.
例題
すべて開く すべて閉じるスコープ (21)
グラフィックス (11)
アプリケーション (8)
RegionBoundsで境界ボックスを作る:
Volumeの相違を計算する:
特性と関係 (8)
Transposeを使ってCuboidを範囲指定に変換する:
逆に,範囲指定をCuboid指定に変換する:
Rotateを使ってGraphics3D中の可能なすべての直方体を得る:
HexahedronはCuboidを一般化したものである:
ImplicitRegionは任意のCuboidを表すことができる:
Parallelepipedは任意のCuboidを表すことができる:
Cuboidは,![]() ノルムについてのノルム球である:
ノルムについてのノルム球である:
関連項目
Cube Hexahedron Parallelogram Rectangle Simplex Polyhedron CanonicalizePolyhedron BoundingRegion
形式: VTK
Function Repository: RoundedCuboid
テクニカルノート
関連するガイド
-
▪
- グラフィックスオブジェクト ▪
- 基本的な特殊領域 ▪
- 立体幾何学 ▪
- 記号的なグラフィックス言語 ▪
- 多面体
履歴
1991 で導入 (2.0) | 2014 で更新 (10.0) ▪ 2019 (12.0)
テキスト
Wolfram Research (1991), Cuboid, Wolfram言語関数, https://reference.wolfram.com/language/ref/Cuboid.html (2019年に更新).
CMS
Wolfram Language. 1991. "Cuboid." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Cuboid.html.
APA
Wolfram Language. (1991). Cuboid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Cuboid.html
BibTeX
@misc{reference.wolfram_2025_cuboid, author="Wolfram Research", title="{Cuboid}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Cuboid.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_cuboid, organization={Wolfram Research}, title={Cuboid}, year={2019}, url={https://reference.wolfram.com/language/ref/Cuboid.html}, note=[Accessed: 18-February-2026]}

