CylindricalDecomposition
CylindricalDecomposition[expr,{x1,x2,…}]
文 expr で表される領域を連続する xiの方向に対応した円柱部分へと分割する.
CylindricalDecomposition[expr,{x1,x2,…},op]
文 expr で表される領域に位相操作 op を適用した結果の分解を求める.
CylindricalDecomposition[expr,{x1,x2,…},"Function"]
後の計算で使用できる結果をCylindricalDecompositionFunction[…][x1,x2,…]として表す.
詳細とオプション



- 文 expr は以下の任意の論理結合でよい.
-
lhs==rhs 等式 lhs!=rhs 等式ではない lhs>rhs または lhs>=rhs 不等式 CylindricalDecompositionFunction[…][x,y,…] 円柱代数式 ForAll[x,cond,expr] 全称記号 Exists[x,cond,expr] 存在記号 - 等式と不等式は,多項式,有理関数,実代数関数を含むことがある.
- CylindricalDecompositionはすべての変数が実数であると仮定する.
- CylindricalDecompositionは一般に上下限に代数関数を含むような不等式を返す.
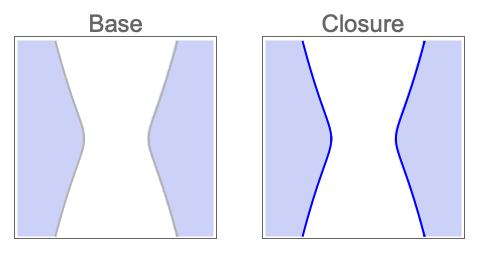
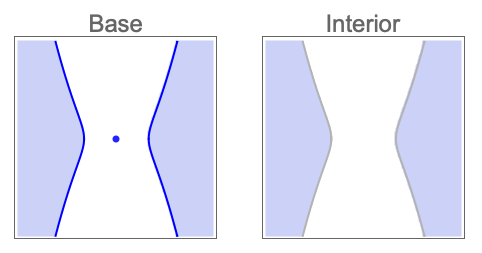
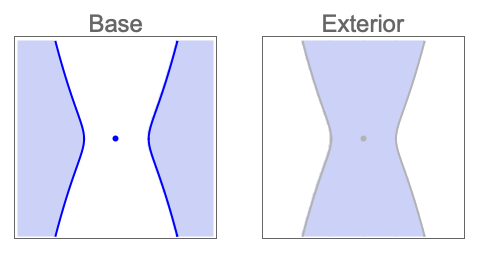
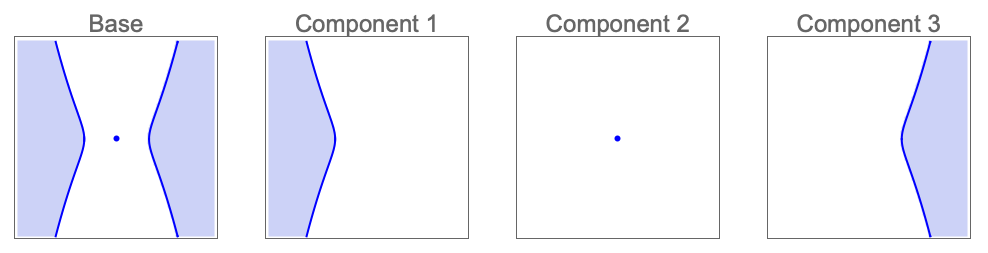
- 位相操作 op は次のいずれかである.
-
"Boundary" 解集合の境界 "Closure" 解集合の閉包 "Interior" 解集合の内側 "Exterior" 解集合の外側 "ClosureOfInterior" 解集合の内側の閉包 "InteriorOfClosure" 解集合の閉包の内側 "Components" 解集合の連結成分 - CylindricalDecompositionFunctionオブジェクトは,さらなる計算で効率的に使用できる半代数集合の明示的なコンパクト表現を提供する.
- CylindricalDecompositionFunctionオブジェクトは,通常,集合のブール値の組合せの計算,追加の条件による集合の制限,一部の変数の削除,集合の最適化等,半代数集合を使用した繰り返しの計算に使用される.
- x1,…,xnにおける円柱代数式は
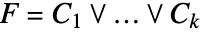 の形をしている.ただし,
の形をしている.ただし,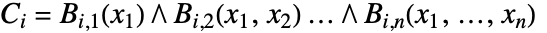 である.各
である.各 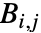 の形は
の形は 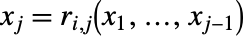 または
または 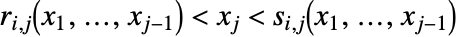 である.ただし
である.ただし 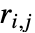 と
と 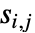 は,
は,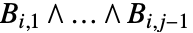 の解集合上で定義され連続代数関数である.
の解集合上で定義され連続代数関数である. 上の
上の 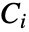 の解集合
の解集合 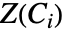 はセルと呼ばれる.セル
はセルと呼ばれる.セル  とセル
とセル  の
の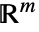 への写像は,任意の
への写像は,任意の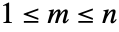 について,互いに素であるか同一であるかのどちらかである.
について,互いに素であるか同一であるかのどちらかである. - CylindricalDecompositionは,"Function"指定がなければ,等式と不等式の論理結合として明示的に書かれた円柱代数式を返す.
- CylindricalDecompositionFunctionは,CylindricalDecompositionの入力として,あるいはReduce,Resolve,FindInstance,Solve,Minimize等のソルバとして使う際にしばしばより効率的な,円柱代数式のカプセル化表現を与える.
- Normalは,CylindricalDecompositionFunctionオブジェクトを,等式と不等式の明示的な論理結合に変換する.
- トポロジー操作と出力形式の指定は組み合せることができる.つまり,CylindricalDecomposition[ineqs,{x1,x2,…},"BoundaryFunction"]は,CylindricalDecompositionFunctionオブジェクトとして表された ineqs の解集合の境界を与える.
例題
すべて開くすべて閉じるスコープ (14)
基本的な用法 (9)
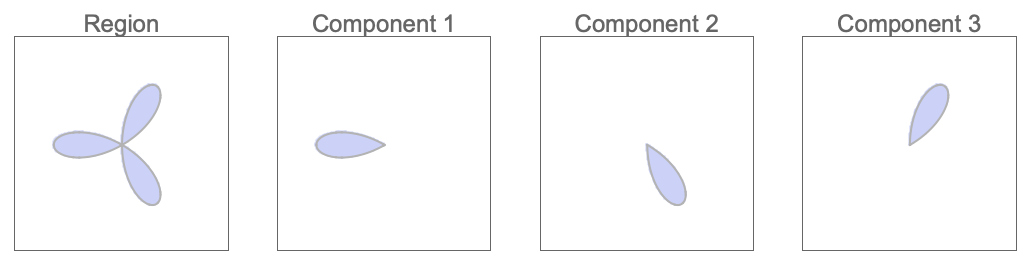
RegionPlotを使って個々の円柱をプロットする:
CylindricalDecompositionには定量化された式を使うことができる:
オプション (1)
WorkingPrecision (1)
WorkingPrecision->1000を使って分解を求めるが,結果が正しくない可能性がある:
特性と関係 (8)
RegionPlotを使って2Dの半代数的集合を可視化する:
RegionPlot3Dを使って3Dの半代数的集合を可視化する:
Resolveは限定子を除去するので,円柱分解の計算を回避できるかもしれない:
これに加え,Reduceは異なる領域と超越関数も扱う:
FindInstanceを使って方程式および不等式を満足する点を求める:
SemialgebraicComponentInstancesは各円柱のサンプル点を与える:
CylindricalDecompositionはいくつかの円柱を組み合せてよりコンパクトに表示する:
GenericCylindricalDecompositionは全次元の部分のみを計算する:
考えられる問題 (2)
テキスト
Wolfram Research (2003), CylindricalDecomposition, Wolfram言語関数, https://reference.wolfram.com/language/ref/CylindricalDecomposition.html (2020年に更新).
CMS
Wolfram Language. 2003. "CylindricalDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/CylindricalDecomposition.html.
APA
Wolfram Language. (2003). CylindricalDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CylindricalDecomposition.html