DirichletL

DirichletL[k,j,s]

对于模 k 和指针 j 的狄利克雷特征 ，给出狄利克雷 L 函数 .

更多信息

  • 整数型数学函数，同时适合符号和数值操作.
  • 对于 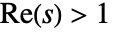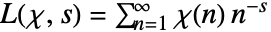， ，其中 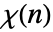是一个狄利克雷特征.
  • 对于模 k 和指针 j 的狄利克雷特征 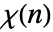，由 DirichletCharacter[k,j,n] 给出.
  • 对于整数 k 和 j，以及任意复数 s，DirichletL[k,j,s] 可求任意数值精度的值.
  • DirichletL 自动线性作用于列表.
  • DirichletL 可与 Interval 和 CenteredInterval 对象一起使用. »

范例

打开所有单元关闭所有单元

基本范例  (2)

沿着线 1+ ω 的图形：

范围  (5)

计算复数参数：

计算高精度：

输出精度与输入精度一致：

自动生成简单精确的值：

DirichletL 按元素线性作用于列表和矩阵的每个元素：

DirichletL 可与 Interval 和 CenteredInterval 对象一起使用：

应用  (4)

绘制临界线上一个 DirichletL 函数的实数部分：

绘制穿过临界带的实数部分：

求出一个 DirichletL 函数的零值：

绘制附近零点的实部和虚部：

巧妙范例  (1)

一个狄利克雷 L 函数的实部：

Wolfram Research (2008)，DirichletL，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DirichletL.html （更新于 2023 年）.

文本

Wolfram Research (2008)，DirichletL，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DirichletL.html （更新于 2023 年）.

CMS

Wolfram 语言. 2008. "DirichletL." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/DirichletL.html.

APA

Wolfram 语言. (2008). DirichletL. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DirichletL.html 年

BibTeX

@misc{reference.wolfram_2024_dirichletl, author="Wolfram Research", title="{DirichletL}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/DirichletL.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dirichletl, organization={Wolfram Research}, title={DirichletL}, year={2023}, url={https://reference.wolfram.com/language/ref/DirichletL.html}, note=[Accessed: 21-December-2024 ]}