![TemplateBox[{s}, DirichletLambda]](Files/DirichletLambda.en/6.png "TemplateBox[{s}, DirichletLambda]"){kind=small}
DirichletLambda
gives the Dirichlet lambda function ![TemplateBox[{s}, DirichletLambda]](Files/DirichletLambda.en/1.png "TemplateBox[{s}, DirichletLambda]"){kind=small}
.
Details
- Mathematical function, suitable for both symbolic and numeric manipulation.
- For
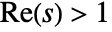, the Dirichlet lambda function is defined as ![TemplateBox[{s}, DirichletLambda]=sum_(n=0)^infty1/((2n+1)^s)](Files/DirichletLambda.en/3.png "TemplateBox[{s}, DirichletLambda]=sum_(n=0)^infty1/((2n+1)^s)")
. - For certain special arguments, DirichletLambda automatically evaluates to exact values.
- DirichletLambda has no branch cut discontinuities.
- DirichletLambda can be evaluated to arbitrary numerical precision.
- DirichletLambda automatically threads over lists.
Examples
open all close allBasic Examples (4)
Scope (8)
DirichletLambda is not an analytic function:
DirichletLambda has both singularity and discontinuity at x=1:
DirichletLambda is meromorphic:
DirichletLambda is neither non-decreasing nor non-increasing:
DirichletLambda is not injective:
DirichletLambda is neither non-negative nor non-positive:
DirichletLambda is neither convex nor concave:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix DirichletLambda function using MatrixFunction:
Properties & Relations (1)
Verify the interrelationship among the DirichletLambda, DirichletEta and Zeta functions:
Text
Wolfram Research (2014), DirichletLambda, Wolfram Language function, https://reference.wolfram.com/language/ref/DirichletLambda.html.
CMS
Wolfram Language. 2014. "DirichletLambda." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DirichletLambda.html.
APA
Wolfram Language. (2014). DirichletLambda. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletLambda.html