WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

DiscreteMinLimit
✖
DiscreteMinLimit

✖
DiscreteMinLimit[f,k∞]

gives the min limit k∞f(k) of the sequence f as k tends to ∞ over the integers.

✖
DiscreteMinLimit[f,{k1,…,kn}]

gives the nested min limit ⋯ f(k1,…,kn) over the integers.

✖
DiscreteMinLimit[f,{k1,…,kn}{,…,}]

gives the multivariate min limit f(k1,…,kn) over the integers.

Details and Options

  • DiscreteMinLimit is also known as limit inferior, infimum limit, liminf, lower limit and inner limit.
  • DiscreteMinLimit computes the largest lower bound for the limit and is always defined for real-valued sequences. It is often used to give conditions of convergence and other asymptotic properties that do not rely on an actual limit to exist.
  • DiscreteMinLimit[f,k∞] can be entered as 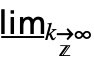f. A template 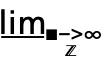can be entered as dmlim, and moves the cursor from the underscript to the body.
  • DiscreteMinLimit[f,{k1,…,kn}{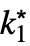,…,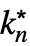}] can be entered as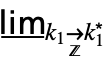…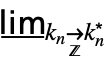f.
  • The possible limit points 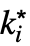are ±∞.
  • The min limit is defined as a limit of the min envelope sequence min[ω]:
  • DiscreteMinLimit[f,k∞]DiscreteLimit[min[ω],ω∞]
    DiscreteMinLimit[f,{k1,…,kn}{∞,…,∞}]DiscreteLimit[min[ω],ω∞]
  • DiscreteMinLimit[f[k],k-∞] is equivalent to DiscreteMinLimit[f[-l],l∞] etc.
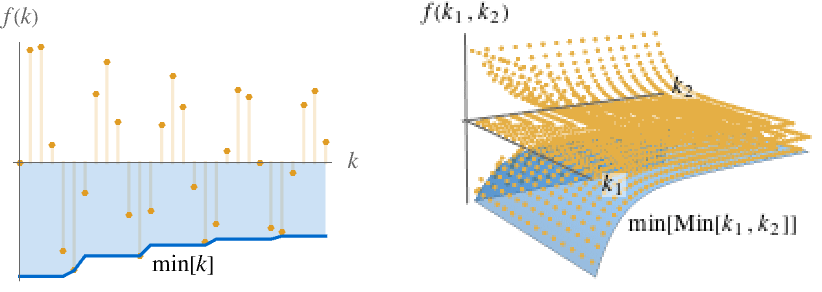
  • The definition uses the min envelope min[ω]MinValue[{f[k],k≥ω∧k∈},k] for univariate f[k] and min[ω]MinValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈},{k1,…,kn}] for multivariate f[k1,…,kn]. The sequence min[ω] is monotone increasing as ω∞, so always has a limit, which may be ±∞.
  • The illustration shows min[k] and min[Min[k1,k2]] in blue.
  • DiscreteMinLimit returns unevaluated when the min limit cannot be found.
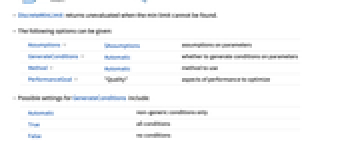
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Automaticwhether to generate conditions on parameters
    Method Automaticmethod to use
    PerformanceGoal "Quality"aspects of performance to optimize
  • Possible settings for GenerateConditions include:
  • Automaticnon-generic conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, DiscreteMinLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Min limit of a sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-g3op6e
Out[1]=1

Min limit of a product:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-khdo7y
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-cz9c26
Out[2]=2

Use dmlim to enter the template and to move from the underscript to the body:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-e1mcaw
Out[1]=1

TraditionalForm typesetting:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-e82anr

Scope  (22)Survey of the scope of standard use cases

Basic Uses  (4)

Compute the min limit of a sequence when n approaches Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-hb5uiw
Out[1]=1

Compute the min limit of a sequence when n approaches -Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-et7bpy
Out[1]=1

Compute a nested limit for a multivariate sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-pukp4y
Out[1]=1

Compute the limit of a list of sequences:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-g45pgr
Out[1]=1

Elementary Function Sequences  (6)

Find the min limit of a rational-exponential sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-lxbke9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-c6vm2a
Out[2]=2

Convergent geometric sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-dc9wk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-f0lb99
Out[2]=2

Oscillating geometric sequence:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-b9ebzb
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-bs2twv
Out[4]=4

Divergent oscillating geometric sequence:

In[5]:=5
✖
https://wolfram.com/xid/0btnx6zdpl8y-q2dwr
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0btnx6zdpl8y-g2hriz
Out[6]=6

Exponential sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-fxkte2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-ek16lf
Out[2]=2

Power sequence:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-i5h5nm
Out[3]=3

Trigonometric sequences:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-e5uei
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-dm6ege
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-ml1zl
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-g527az
Out[4]=4

Inverse trigonometric sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-lykjl
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-yzua9
Out[2]=2

Logarithmic sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-8qd0z
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-i4pw3x
Out[2]=2

Integer Function Sequences  (3)

Sequences involving Factorial:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-yem9f
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-1sstox
Out[2]=2

Sequence involving FactorialPower:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-bof7hm
Out[1]=1

Compute the limit of a sequence involving Fibonacci:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-bcqotc
Out[1]=1

Periodic Sequences  (3)

Limits of periodic sequences:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-clh32t
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-ilo0ri
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-f0qvyn
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-egrxv
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0btnx6zdpl8y-d03d2h
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0btnx6zdpl8y-gnytrw
Out[6]=6

Eventually periodic sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-cpqsv5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-k12ere
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-f6lwfg
Out[3]=3

Densely aperiodic sequences:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-d7z025
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-k07f3o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-lmhs11
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-bzcdcc
Out[4]=4

Piecewise Function Sequences  (2)

Piecewise sequence with a finite min limit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-vznig
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-kkguvr
Out[2]=2

Piecewise sequence with an infinite min limit:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-xejfm
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-m4nvru
Out[4]=4

Piecewise sequence with periodic conditions:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-d9ybuq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-skkms
Out[2]=2

Number Theoretic Sequences  (2)

Limits involving LCM and GCD:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-b1qh0b
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-bitj2u
Out[2]=2

Sequence involving Prime:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-fsldo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-c9987h
Out[2]=2

Multivariate Sequences  (2)

Compute a nested min limit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-b08k82
Out[1]=1

Plot the sequence and its limit:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-bx7d8j
Out[2]=2

Multivariate min limits:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-yctew
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-icispr
Out[2]=2

Options  (6)Common values & functionality for each option

Assumptions  (1)

Specify assumptions on a parameter:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-e8anyf
Out[1]=1

Different assumptions can produce different results:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-hwqo5k
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-bwcs4h
Out[3]=3

GenerateConditions  (3)

Return a result without stating conditions:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-spbhce
Out[1]=1

This result is only valid if x>1:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-lftbu6
Out[1]=1

Return unevaluated if the results depend on the value of parameters:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-2lepxp
Out[1]=1

By default, conditions are generated that return a unique result:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-14nrvk
Out[2]=2

By default, conditions are not generated if only special values invalidate the result:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-uhm6gw
Out[1]=1

With GenerateConditions->True, even these non-generic conditions are reported:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-291b1m
Out[2]=2

Method  (1)

Compute the min limit of a periodic sequence using the default method:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-gna87y
Out[1]=1

Obtain the same answer using the method for periodic sequences:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-jt0cjx
Out[2]=2

The limit of the sequence is undefined, since it oscillates between 0 and 1:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-eqc0mj
Out[3]=3

PerformanceGoal  (1)

DiscreteMinLimit computes limits involving sequences of arbitrarily large periods:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-i86kxj
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-i9gq
Out[2]=2

Use PerformanceGoal to avoid potentially expensive computations in such cases:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-byiylb
Out[3]=3

The Method option overrides PerformanceGoal:

In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-bh9kxc
Out[4]=4

Applications  (3)Sample problems that can be solved with this function

Compute the asymptotic minimum of a sequence:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-evnfw9
Out[1]=1

Plot the sequence and the asymptotic minimum:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-dxedrx
Out[2]=2

Verify that the following sequence does not have a limit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-cy4wh5
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-bibaa2
Out[2]=2

Show that DiscreteMaxLimit and DiscreteMinLimit are not equal:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-wrhna
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-d48yo1
Out[4]=4

Confirm that the limit does not exist by using DiscreteLimit:

In[5]:=5
✖
https://wolfram.com/xid/0btnx6zdpl8y-esjhm8
Out[5]=5

An algorithm runtime function is said to be "big-omega of ", written , if _(n->_(TemplateBox[{}, Integers])infty) (f(n))/(g(n))>0:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-mlj236

Similarly, is said to be "big-theta of ", written if _(n->_(TemplateBox[{}, Integers])infty) (f(n))/(g(n))<infty and _(n->_(TemplateBox[{}, Integers])infty)(f(n))/(g(n))>0:

In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-ofku20

The statement is always true:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-bv5n1w
Out[3]=3

If and , then :

In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-n96r3n
Out[4]=4

It is possible for two functions to share neither relationship:

In[5]:=5
✖
https://wolfram.com/xid/0btnx6zdpl8y-z3kbhh
Out[5]=5

Hence, defines a reflexive partial order on the space of algorithm runtimes similar to :

In[6]:=6
✖
https://wolfram.com/xid/0btnx6zdpl8y-wowly
In[7]:=7
✖
https://wolfram.com/xid/0btnx6zdpl8y-sh3ntl
Out[7]=7

If and , then , which implies that is an equivalence relation:

In[8]:=8
✖
https://wolfram.com/xid/0btnx6zdpl8y-dezmtj
Out[8]=8

Properties & Relations  (11)Properties of the function, and connections to other functions

A real-valued function always has a (possibly infinite) min limit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-dqn5f4
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-ejovu
Out[2]=2

The corresponding limit may not exist:

In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-9h2du
Out[3]=3

If and have finite min limits, then TemplateBox[{{(, {f, +, g}, )}, x, a}, DiscreteMinLimit]>=TemplateBox[{f, x, a}, DiscreteMinLimit]+TemplateBox[{g, x, a}, DiscreteMinLimit]:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-hapf7s
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-ki9asl
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-hoyphw
Out[3]=3

In this case, there is strict inequality:

In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-4wm4fg
Out[4]=4

Positive multiplicative constants can be moved outside a limit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-bytgex
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-fv4gx
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-crrr33
Out[3]=3

For a real-valued sequence, if DiscreteLimit exists, DiscreteMinLimit has the same value:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-djj1nf
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-tlom4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-bb2v
Out[3]=3

If has a finite limit, then TemplateBox[{{(, {f, +, g}, )}, x, a}, DiscreteMinLimit]=TemplateBox[{f, x, a}, DiscreteMinLimit]+TemplateBox[{g, x, a}, DiscreteMinLimit]:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-hfqnkd
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-jeu5t4
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-5nd1ru
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-hi3dhc
Out[4]=4

DiscreteMinLimit is less than or equal to DiscreteMaxLimit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-cxy11z
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-iehyz0
Out[2]=2

If DiscreteMinLimit equals DiscreteMaxLimit, the limit exists and equals their common value:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-f6hztd
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-bvlaz9
Out[2]=2

If the min limit is , then the max limit and thus the limit are also :

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-tw9zq1
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-1z7ub5
Out[2]=2

DiscreteMinLimit can be computed as -DiscreteMaxLimit[-f,…]:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-5oz4gv
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-mse78t
Out[2]=2

If , then TemplateBox[{{g, (, n, )}, x, a}, MinLimit2Arg]>=TemplateBox[{{f, (, n, )}, x, a}, MaxLimit2Arg]>=TemplateBox[{{f, , {(, n, )}}, x, a}, MinLimit2Arg]:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-zwywc
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-g2avgr
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-wbzb2v
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-k7j3pk
Out[4]=4

If the two max limits are equal—as in this example—then has a limit:

In[5]:=5
✖
https://wolfram.com/xid/0btnx6zdpl8y-vnttqn
Out[5]=5

This is a generalization of the "squeezing" or "sandwich" theorem:

In[6]:=6
✖
https://wolfram.com/xid/0btnx6zdpl8y-b1meus
Out[6]=6

MinLimit is always less than or equal to DiscreteMinLimit:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-58ji5s
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-34gpyb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-qtl6qs
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0btnx6zdpl8y-uu7jv3
Out[4]=4

Possible Issues  (1)Common pitfalls and unexpected behavior

DiscreteMinLimit is only defined for real-valued sequences:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-kyusc
Out[1]=1

Neat Examples  (1)Surprising or curious use cases

Visualize a set of sequence min limits:

In[1]:=1
✖
https://wolfram.com/xid/0btnx6zdpl8y-cd80wk
In[2]:=2
✖
https://wolfram.com/xid/0btnx6zdpl8y-hq7d3z
In[3]:=3
✖
https://wolfram.com/xid/0btnx6zdpl8y-xvse5
Out[3]=3
Wolfram Research (2017), DiscreteMinLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.
✖
Wolfram Research (2017), DiscreteMinLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.

Text

Wolfram Research (2017), DiscreteMinLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.

✖
Wolfram Research (2017), DiscreteMinLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.

CMS

Wolfram Language. 2017. "DiscreteMinLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.

✖
Wolfram Language. 2017. "DiscreteMinLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMinLimit.html.

APA

Wolfram Language. (2017). DiscreteMinLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMinLimit.html

✖
Wolfram Language. (2017). DiscreteMinLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMinLimit.html

BibTeX

@misc{reference.wolfram_2025_discreteminlimit, author="Wolfram Research", title="{DiscreteMinLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMinLimit.html}", note=[Accessed: 24-April-2025 ]}

✖
@misc{reference.wolfram_2025_discreteminlimit, author="Wolfram Research", title="{DiscreteMinLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMinLimit.html}", note=[Accessed: 24-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_discreteminlimit, organization={Wolfram Research}, title={DiscreteMinLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteMinLimit.html}, note=[Accessed: 24-April-2025 ]}

✖
@online{reference.wolfram_2025_discreteminlimit, organization={Wolfram Research}, title={DiscreteMinLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteMinLimit.html}, note=[Accessed: 24-April-2025 ]}