WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

DrazinInverse[m]

正方行列 m の一般化された逆行列 を求める．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
基本的な用法  
特殊行列  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

DrazinInverse

DrazinInverse[m]

正方行列 m の一般化された逆行列 を求める．

詳細とオプション

  • 正方行列 m のDrazin逆行列は，m の不変部分空間に基づく一般化された逆行列である．
  • Drazin逆行列は，Moore–Penrose逆行列が一般化された逆行列であるように，一般化された逆行列である．しかし，Drazin逆行列は不変部分空間を扱い，固有値問題，微分方程式および差分方程式の解等と関連しているのに対し， Moore–Penrose逆行列は最小二乗問題を扱い，フィッティング，特異値分解，近似等と関連がある．
  • DrazinInverse[m]は t.(TemplateBox[{c}, Inverse] 0; 0 0).TemplateBox[{t}, Inverse]として計算することができる．ただし，{t,c,n}はCoreNilpotentDecomposition[m]によって返されたリストである． »
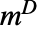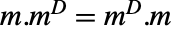  • Drazin逆行列 は と 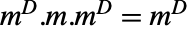の関係を満足する． »
  • 行列のベキ零指標 は零固有値に対応する最大ジョルダン(Jordan)ブロックのサイズとして定義される．Drazin逆行列 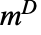は関係 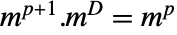を満足する．ただし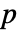， は m のベキ零指標である． »
  • 正則正方行列 m について，Drazin逆行列 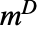は標準的な逆行列に等しい．
  • DrazinInverse[m]は，StandardFormとTraditionalFormでは とフォーマットされる． »

例題

すべて開く すべて閉じる

例  (3)

行列のDrazin逆行列を計算する：

Wolfram Language code: DrazinInverse[(⁠| | | | | - | - | - | | 1 | 2 | 0 | | 5 | 1 | 3 | | 0 | 0 | 0 |⁠)]//MatrixForm

3×3行列のDrazin逆行列：

Wolfram Language code: m = {{2, 0, 0}, {-1, 1 / 5, 1}, {-1 / 3, -1, -1}};
Wolfram Language code: (d = DrazinInverse[m])//MatrixForm

一般化された逆行列のいくつかの特性を検証する：

Wolfram Language code: d.m == m.d
Wolfram Language code: d.m.d == d

4×4行列のDrazin逆行列：

Wolfram Language code: m = {{-2, 5, 4, 4}, {3, -3, -3, -4}, {-4, 1, 2, 4}, {-2, 4, 5, 3}};
Wolfram Language code: (d = DrazinInverse[m])//MatrixForm

DrazinInverseの定義を確認する：

Wolfram Language code: {t, c, n} = CoreNilpotentDecomposition[m];
Wolfram Language code: a = PadRight[Inverse[c], Dimensions[m]];
Wolfram Language code: d === t.a.Inverse[t]

スコープ  (11)

基本的な用法  (7)

機械精度行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[{{0.2, -0.32}, {0.1, -0.16}}]

複素行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[{{-4 + 6 I, 8 - 10 I, 2}, {-2 + 3 I, 4 - 5 I, 1}, {1, -1, 1}}]

厳密行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[{{1, 2, -2}, {4, 5, -3}, {1, 5, -3}}]

任意精度行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[RandomReal[4, {2, 2}, WorkingPrecision -> 20]]

記号行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[{{a, a, 1}, {0, 0, 0}, {2, 3, -1}}]//Simplify

大きい機械精度行列の反転は効率的である：

Wolfram Language code: mat = RandomReal[{0, 10}, {800, 800}];
Wolfram Language code: AbsoluteTiming[DrazinInverse[mat];]

出力のフォーマット：

Wolfram Language code: DrazinInverse[m]

特殊行列  (4)

疎な行列のDrazin逆行列は正規行列として返される：

Wolfram Language code: SparseArray[{{1, 3} -> 1, {2, 2} -> 2, {3, 1} -> 3}, {3, 3}]
Wolfram Language code: DrazinInverse[%]

構造化行列のDrazin逆行列：

Wolfram Language code: SymmetrizedArray[{{1, 1} -> 3, {2, 2} -> 1, {3, 1} -> -5}, {3, 3}, Symmetric[All]]
Wolfram Language code: DrazinInverse[%]

IdentityMatrixはそれ自体のDrazin逆行列である：

Wolfram Language code: DrazinInverse[IdentityMatrix[3]]

ヒルベルト(Hilbert)行列のDrazin逆行列：

Wolfram Language code: DrazinInverse[HilbertMatrix[3]]

アプリケーション  (3)

特異係数を持つ行列微分方程式 , を解く：

Wolfram Language code: a = (| | | | | -- | - | -- | | 1 | 0 | -2 | | -1 | 0 | 2 | | 2 | 3 | 2 |);b = (| | | | | --- | --- | --- | | 0 | 1 | 2 | | -27 | -22 | -17 | | 18 | 14 | 10 |);v = {-1, -8, 13};

と はどちらも特異なので，この方程式は標準形 にはできない：

Wolfram Language code: {Det[a], Det[b]}

解は である．ただし， は を， は を解く：

Wolfram Language code: MatrixExp[-DrazinInverse[LinearSolve[a + b, a]].LinearSolve[a + b, b]t].v//Simplify

DSolveValueが与える結果と比較する：

Wolfram Language code: DSolveValue[{a.y'[t] + b.y[t] == 0, y[0] == v}, y[t]∈Vectors[3], t]

特異係数行列 を持つ行列差分方程式 の一般解を求める：

Wolfram Language code: m = (⁠| | | | | -- | -- | -- | | 4 | 2 | -2 | | -8 | -3 | 1 | | -6 | -2 | 0 |⁠);

行列 は特異行列である：

Wolfram Language code: Det[m]

解は である．ただし， は任意のベクトルである：

Wolfram Language code: x[n_] = Simplify[MatrixPower[DrazinInverse[m], n + 1].m.{C[1], C[2], C[3]}, n > 0]

解を検証する：

Wolfram Language code: m.x[n + 1] == x[n]//Simplify

グラフの事実上の抵抗行列を計算する：

Wolfram Language code: g = [image];
Wolfram Language code: MatrixForm[rm = With[{n = VertexCount[g], km = Normal[KirchhoffMatrix[g]]}, Table[ReplacePart[Diagonal[DrazinInverse[ReplacePart[km, k -> UnitVector[n, k]]]], k -> 0], {k, n}]]]

事実上のグラフ抵抗を計算する：

Wolfram Language code: Total[rm, 2] / 2

特性と関係  (8)

DrazinInverseは可逆行列についてはInverseと同じである：

Wolfram Language code: m = {{2, 5}, {7, 18}};
Wolfram Language code: DrazinInverse[m]
Wolfram Language code: Inverse[m]

DrazinInverse[m]は と の関係を満足する：

Wolfram Language code: m = {{0, 1, 0}, {0, 1, 1}, {0, 0, 0}};
Wolfram Language code: (d = DrazinInverse[m])//MatrixForm

必要とされる特性を検証する：

Wolfram Language code: d.m == m.d
Wolfram Language code: d.m.d == d

PseudoInverseとは異なり，必ずしも である訳ではない：

Wolfram Language code: m.d.m == m

ムーア・ペンローズ(Moore–Penrose)方程式[詳細]を満足する必要もない：

Wolfram Language code: {m.d == (m.d), d.m == (m.d)}

DrazinInverseは，行列随伴のもとでは可逆である，すなわち(a.b.TemplateBox[{a}, Inverse])^D=a.b^D.TemplateBox[{a}, Inverse]：

Wolfram Language code: a = {{8, 7, 0}, {9, 9, 2}, {9, 4, 7}}; b = {{6, 7, 6}, {5, 8, 5}, {1, 6, 4}};
Wolfram Language code: DrazinInverse[a.b.Inverse[a]] == a.DrazinInverse[b].Inverse[a]

DrazinInverseはCoreNilpotentDecompositionで計算できる：

Wolfram Language code: m = {{-6, -3, -4, 2}, {0, -1, 0, 1}, {9, 6, 6, -2}, {0, 4, 0, 1}};
Wolfram Language code: {t, c, n} = CoreNilpotentDecomposition[m];
Wolfram Language code: d = DrazinInverse[m];

等式 m^D=t.(TemplateBox[{c}, Inverse] 0; 0 0).TemplateBox[{t}, Inverse]を確かめる：

Wolfram Language code: d === t.PadRight[Inverse[c], Dimensions[m]].Inverse[t]

DrazinInverse[m]は，対角行列 m について非零の要素が反転された対角行列である：

Wolfram Language code: DrazinInverse[DiagonalMatrix[{3, 14, 0}]]//MatrixForm

JordanDecomposition[m]で与えられたジョルダン行列 について考える：

Wolfram Language code: m = (⁠| | | | | | - | - | -- | -- | | 2 | 6 | -9 | -2 | | 6 | 6 | -3 | -6 | | 0 | 0 | 4 | 0 | | 2 | 6 | -9 | -2 |⁠); {s, j} = JordanDecomposition[m];

DrazinInverseは対角要素が0のブロックを0にマップし，他のブロックをその逆数にマップする：

Wolfram Language code: {j//MatrixForm, DrazinInverse[j]//MatrixForm}

さらに，m^D=s.j^D.TemplateBox[{s}, Inverse]である：

Wolfram Language code: DrazinInverse[m] == s.DrazinInverse[j].Inverse[s]

正方行列の指標を計算する関数を定義する：

Wolfram Language code: matrixIndex[m_ ? SquareMatrixQ] := Length[NestWhileList[m.#&, IdentityMatrix[Length[m]], MatrixRank[#1] != MatrixRank[#2]&, 2]] - 2

行列の指標を計算する：

Wolfram Language code: m = {{4, 2, -2}, {-5, -3, 4}, {-3, -2, 3}};
Wolfram Language code: k = matrixIndex[m]

DrazinInverse[m]は という関係を満足する．ただし，k は m の指標である：

Wolfram Language code: MatrixPower[m, k + 1].DrazinInverse[m] == MatrixPower[m, k]

PseudoInverseはDrazinInverseによって TemplateBox[{{{{m, ^, {(, {(, {-, 1}, )}, )}}, =, {TemplateBox[{{(, m}}, ConjugateTranspose], ., m}}, )}, D}, Superscript].TemplateBox[{m}, ConjugateTranspose]と表すことができる：

Wolfram Language code: m = {{2, 2, -2}, {5, 1, -3}, {1, 5, -3}};
Wolfram Language code: PseudoInverse[m] == DrazinInverse[ConjugateTranspose[m].m].ConjugateTranspose[m]
Wolfram Research (2021), DrazinInverse, Wolfram言語関数， https://reference.wolfram.com/language/ref/DrazinInverse.html （2025年に更新）.

テキスト

Wolfram Research (2021), DrazinInverse, Wolfram言語関数， https://reference.wolfram.com/language/ref/DrazinInverse.html （2025年に更新）.

CMS

Wolfram Language. 2021. "DrazinInverse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/DrazinInverse.html.

APA

Wolfram Language. (2021). DrazinInverse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DrazinInverse.html

BibTeX

@misc{reference.wolfram_2026_drazininverse, author="Wolfram Research", title="{DrazinInverse}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/DrazinInverse.html}", note=[Accessed: 01-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_drazininverse, organization={Wolfram Research}, title={DrazinInverse}, year={2025}, url={https://reference.wolfram.com/language/ref/DrazinInverse.html}, note=[Accessed: 01-August-2026]}