DrazinInverse
找到方阵 m 的 Drazin 广义逆 ![]() .
.
更多信息和选项

- 方阵 m 的 Drazin 逆是基于 m 的不变子空间的广义逆.
- Drazin 逆是广义逆,就像 Moore– Penrose 逆是广义逆一样. 然而,Drazin 逆处理不变子空间,并涉及特征值问题、微分方程和差分方程的解等,而 Moore– Penrose 逆处理的是最小二乘并涉及拟合问题、SVD、逼近等.
- DrazinInverse[m] 可以计算为
![t.(TemplateBox[{c}, Inverse] 0; 0 0).TemplateBox[{t}, Inverse] t.(TemplateBox[{c}, Inverse] 0; 0 0).TemplateBox[{t}, Inverse]](Files/DrazinInverse.zh/2.png) ,其中 {t,c,n} 是由 CoreNilpotentDecomposition[m] 返回的列表. »
,其中 {t,c,n} 是由 CoreNilpotentDecomposition[m] 返回的列表. » - Drazin 逆
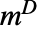 满足关系
满足关系 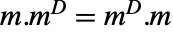 和
和 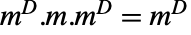 . »
. » - 矩阵的幂零指数
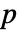 定义为对应于零特征值的最大约当块的大小. Drazin 逆
定义为对应于零特征值的最大约当块的大小. Drazin 逆 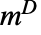 满足关系
满足关系 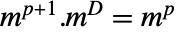 ,其中
,其中 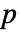 是 m 的幂零指数. »
是 m 的幂零指数. » - 对于非奇异方阵 m,Drazin 逆
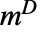 等价于标准逆.
等价于标准逆. - DrazinInverse[m] formats as
 in StandardForm and TraditionalForm. »
in StandardForm and TraditionalForm. »
范例
打开所有单元 关闭所有单元基本范例 (3)
范围 (11)
基本用法 (7)
特殊矩阵 (4)
应用 (3)
与 DSolveValue 给出的结果进行比较:
属性和关系 (8)
DrazinInverse 与可逆矩阵的 Inverse 相同:
DrazinInverse[m] 满足关系 ![]() 和
和 ![]() :
:
与 PseudoInverse 不同,![]() 不一定是这种情况:
不一定是这种情况:
另一个 Moore–Penrose 方程 [更多信息] 不需满足:
DrazinInverse 在矩阵共轭下是不变的,即 ![]() :
:
DrazinInverse 可以通过 CoreNilpotentDecomposition 计算:
对于对角矩阵 m,DrazinInverse[m] 是非零元素反转的对角矩阵:
考虑 JordanDecomposition[m] 给出的约当矩阵 ![]() :
:
DrazinInverse 将具有零对角线的块映射到零,将其他块映射到它们的逆:
DrazinInverse[m] 满足关系 ![]() ,其中 k 是 m 的索引:
,其中 k 是 m 的索引:
PseudoInverse[m] 可以使用 DrazinInverse 计算为 ![]() :
:
相关指南
-
▪
- 线性系统
文本
Wolfram Research (2021),DrazinInverse,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DrazinInverse.html (更新于 2025 年).
CMS
Wolfram 语言. 2021. "DrazinInverse." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/DrazinInverse.html.
APA
Wolfram 语言. (2021). DrazinInverse. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DrazinInverse.html 年
BibTeX
@misc{reference.wolfram_2025_drazininverse, author="Wolfram Research", title="{DrazinInverse}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/DrazinInverse.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_drazininverse, organization={Wolfram Research}, title={DrazinInverse}, year={2025}, url={https://reference.wolfram.com/language/ref/DrazinInverse.html}, note=[Accessed: 06-February-2026]}

