ElectricCurrentPDEComponent[vars,pars]
yields an electric current PDE term with variables vars and parameters pars.


ElectricCurrentPDEComponent
ElectricCurrentPDEComponent[vars,pars]
yields an electric current PDE term with variables vars and parameters pars.
Details






- ElectricCurrentPDEComponent is typically used to generate an electric current continuity equation with model variables vars and model parameters pars.
- ElectricCurrentPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- ElectricCurrentPDEComponent creates PDE components for stationary, frequency and parametric analysis.
- ElectricCurrentPDEComponent models electric fields produced by direct or alternating currents in conductive materials when magnetic and inductive effects are negligible.
- The results of ElectricCurrentPDEComponent can be use to compute current density magnitude values. »
- ElectricCurrentPDEComponent models stationary or harmonic electric fields with the electric scalar potential
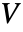 [
[![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/4.png) ] as dependent variable and independent variables
] as dependent variable and independent variables  [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/6.png) ].
]. - Stationary variables vars are vars={V[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={V[t,x1,…,xn],t,{x1,…,xn}}.
- Frequency-dependent variables vars are vars={V[x1,…,xn],ω,{x1,…,xn}}.
- The current continuity equation is
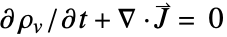 with volume charge density
with volume charge density 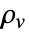 [
[![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/9.png) ], time variable
], time variable 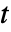 [
[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/11.png) ] and current density vector
] and current density vector 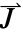 [
[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/13.png) ].
]. - The constitutional material model equation, known as Ohm's law, is
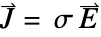 where
where 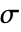 [
[![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/16.png) ] is the electrical conductivity and
] is the electrical conductivity and 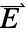 [
[![TemplateBox[{InterpretationBox[, 1], {"V", , "/", , "m"}, volts per meter, {{(, "Volts", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"V", , "/", , "m"}, volts per meter, {{(, "Volts", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/18.png) ] the electric field with
] the electric field with 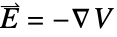 .
. - ElectricCurrentPDEComponent provides a stationary electric current model where
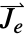 [
[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/21.png) ] is an externally generated current density vector and
] is an externally generated current density vector and 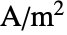 [
[![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/23.png) ] a current source:
] a current source: - ElectricCurrentPDEComponent provides a time domain model with time variable
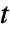 [
[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/26.png) ], vacuum permittivity
], vacuum permittivity 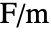 [
[![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/28.png) ] and relative permittivity
] and relative permittivity 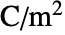 [
[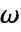 ]:
]: - ElectricCurrentPDEComponent provides a frequency domain model with vacuum permittivity
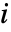 [
[![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/33.png) ], polarization vector
], polarization vector 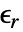 [
[![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/35.png) ], angular frequency
], angular frequency 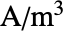 [
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/37.png) ] and the imaginary unit
] and the imaginary unit 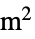 :
: - For linear materials, the frequency domain model simplifies to:
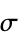 is the unitless relative permittivity.
is the unitless relative permittivity.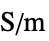 can be isotropic, orthotropic or anisotropic.
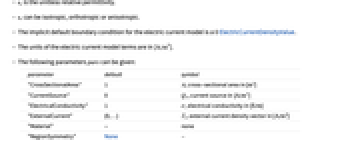
can be isotropic, orthotropic or anisotropic.- The implicit default boundary condition for the electric current model is a 0 ElectricCurrentDensityValue.
- The units of the electric current model terms are in [
![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/43.png) ].
]. - The following parameters pars can be given:
-
parameter default symbol "CrossSectionalArea" 1 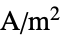 , cross-sectional area in [
, cross-sectional area in [![TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/45.png) ]
] "CurrentSource" 0 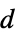 , current source in [
, current source in [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 3}}, amperes per meter cubed, {{(, "Amperes", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/47.png) ]
]"ElectricalConductivity" 1 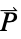 , electrical conductivity in [
, electrical conductivity in [![TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"S", , "/", , "m"}, siemens per meter, {{(, "Siemens", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/49.png) ]
]
"ExternalCurrentSource" {0,…} 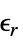 , external current density vector in [
, external current density vector in [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , {"m", ^, 2}}, amperes per meter squared, {{(, "Amperes", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/51.png) ]
]"Material" - none "RegionSymmetry" None 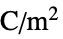
"Thickness" 1 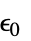 , thickness in [
, thickness in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/54.png) ]
] - If a "Material" is specified, material constants are extracted from the material data; otherwise, relevant material parameters need to be specified.
- Additional parameters can be specified for the frequency domain models:
-
parameter default symbol "Polarization" {0,…} 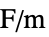 , polarization vector in [
, polarization vector in [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/56.png) ]
]"RelativePermittivity" 1 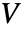 , unitless relative permittivity
, unitless relative permittivity
"RemanentPolarization" {0,…} 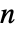 , remanent polarization vector in [
, remanent polarization vector in [![TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/59.png) ]
]"VacuumPermittivity" 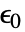
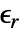 , vacuum permittivity in [
, vacuum permittivity in [![TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"F", , "/", , "m"}, farads per meter, {{(, "Farads", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/ElectricCurrentPDEComponent.en/62.png) ]
] - All parameters may depend on the spacial variable
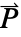 and dependent variable
and dependent variable 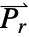 .
. - The number of independent variables
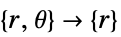 determines the dimensions of
determines the dimensions of 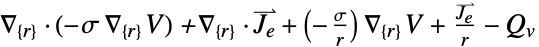 ,
, 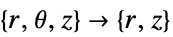 and
and 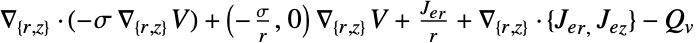 , and the length of vectors
, and the length of vectors 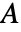 ,
, 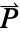 and
and 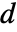 .
. - A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction e.g. stationary equation 1D 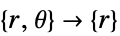
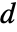
2D 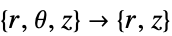
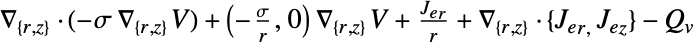
- In 1D, when a "CrossSectionalArea"
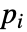 is specified, the ElectricCurrentPDEComponent equation is given as:
is specified, the ElectricCurrentPDEComponent equation is given as: - In 2D, when a "Thickness"
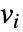 is specified, the ElectricCurrentPDEComponent equation is given as:
is specified, the ElectricCurrentPDEComponent equation is given as: - In a 1D axisymmetric case, when a "Thickness"
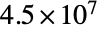 is specified, the ElectricCurrentPDEComponent equation is given as:
is specified, the ElectricCurrentPDEComponent equation is given as: - The input specification for the parameters is exactly the same as for their corresponding operator terms.
- If no parameters are specified, the default electric current PDE is:
- If the ElectricCurrentPDEComponent depends on parameters
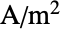 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 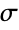 are replaced with
are replaced with 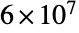 .
.
Examples
open all close allBasic Examples (4)
Scope (8)
Define a symbolic stationary current PDE:
Define a stationary current PDE model for a specific material:
Specify an stationary current PDE with an electrical conductivity of ![]() in units of [
in units of [![]() ] and an external current density of
] and an external current density of ![]() in units of [
in units of [![]() ]:
]:
Activate a stationary current PDE model for a specific material:
Define a symbolic stationary current PDE with electrical conductivity ![]() an external current, a current source and a thickness:
an external current, a current source and a thickness:
Define a symbolic 2D axisymmetric stationary current PDE:
Applications (5)
2D Stationary Analysis (1)
3D Stationary Analysis (3)
Model a copper wire that is excited with a direct current (DC) of ![]() [
[![]() ] with a current density boundary condition at the upper boundary and with a zero electric potential condition at the lower boundary.
] with a current density boundary condition at the upper boundary and with a zero electric potential condition at the lower boundary.
Set up the stationary current PDE model variables ![]() and
and ![]() :
:
Specify ground potential at the lower boundary:
Specify an inward current flow at the upper boundary:
Visualize the electric potential:
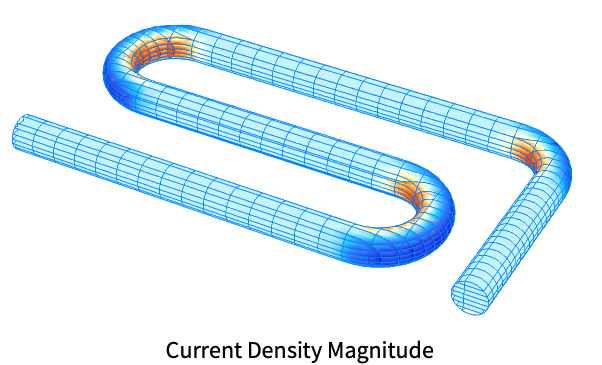
Model a tungsten wire with a potential difference of ![]() [
[![]() ]. Set up the stationary current PDE model variables
]. Set up the stationary current PDE model variables ![]() and
and ![]() :
:
Set up the stationary current PDE:
The radius of the tungsten wire is ![]() [
[![]() ] and the geometric shape of the wire is s-shaped. Specify the parameters of the geometry:
] and the geometric shape of the wire is s-shaped. Specify the parameters of the geometry:
An electric potential boundary condition of ![]() [
[![]() ] is applied at the left end boundary and a zero electric potential condition is applied at the right end boundary. A tolerance 0f
] is applied at the left end boundary and a zero electric potential condition is applied at the right end boundary. A tolerance 0f ![]() is applied at both ends to account for numerical errors in the discretized domain.
is applied at both ends to account for numerical errors in the discretized domain.
Set the electric potential boundary conditions at both ends of the wire:
Compute the current density vector:
Visualize the current density magnitude:
Model a copper spiral inductor that is excited with a current density normal to the left boundary and has a zero electric potential boundary condition at the right boundary.
Define the spiral inductor geometry:
Set up the stationary current PDE model variables ![]() and
and ![]() :
:
Specify an inward current flow on the left boundary:
Frequency Analysis (1)
Model a dielectric material of a cylindrical capacitor that is excited with an alternating current (AC) of ![]() [
[![]() ], with a current density boundary condition at the upper electrode, and with a zero electric potential boundary condition at the lower boundary.
], with a current density boundary condition at the upper electrode, and with a zero electric potential boundary condition at the lower boundary.
Set up the frequency current PDE model variables ![]() :
:
Define the frequency and the period:
Specify an electrical conductivity ![]() and a relative permittivity
and a relative permittivity ![]() :
:
Specify the ground potential at the lower boundary:
Specify an inward current flow at the upper boundary:
Solve the harmonic PDE for ![]() [
[![]() ]:
]:
Transform the voltage at the upper boundary to the time domain:
Possible Issues (2)
For a symbolic computation, the "ElectricalConductivity", "VacuumPermittivity" or "RelativePermittivity" parameters should be given as a matrix:
For numeric values, the "ElectricalConductivity", "VacuumPermittivity" or "RelativePermittivity" parameter is automatically converted to a matrix of proper dimensions:
This automatic conversion is not possible for symbolic input:
Not providing the properly dimensioned matrix will result in an error:
For frequency domain models, material parameters are not available when "Material" is specified:
Tech Notes
Related Guides
Text
Wolfram Research (2024), ElectricCurrentPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html (updated 2025).
CMS
Wolfram Language. 2024. "ElectricCurrentPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html.
APA
Wolfram Language. (2024). ElectricCurrentPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_electriccurrentpdecomponent, author="Wolfram Research", title="{ElectricCurrentPDEComponent}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_electriccurrentpdecomponent, organization={Wolfram Research}, title={ElectricCurrentPDEComponent}, year={2025}, url={https://reference.wolfram.com/language/ref/ElectricCurrentPDEComponent.html}, note=[Accessed: 08-January-2026]}