Equal

lhs==rhs

lhs と rhs が同じである場合，Trueを返す．

詳細

  • lhs==rhs は，Solveのような関数を使って操作する記号方程式を表すときに使われる．
  • lhs==rhs は，lhs と rhs が通常の同じ式である場合，Trueを返す．
  • lhs==rhs は，lhs と rhs が，数または他の未加工データ（文字列等）を比較した上で等しくないと判断された場合，Falseを返す．
  • 機械精度あるいはそれ以上の精度の近似数は，二進法表記で最後の7桁までは異なっても等しいとされる（十進法表記では最後の2桁程度）．
  • 機械精度よりも精度の低い数の場合，要求される許容度は数の精度に比例して小さくなる．
  • 2==2.は，Trueを与える．
  • e1==e2==e3 は，ei が等しい場合にTrueを与える．
  • Equal[e]はTrueを与える．
  • 厳密な数値に対して，Equalは不等式を成立させるために数値近似値を使う．この過程は大域変数$MaxExtraPrecisionの影響を受ける．
  • lhs または rhs がIndeterminateやOverflow等のオブジェクトを含んでいる場合，Equalは未評価で残される．
  • StandardFormやInputFormにおいて，lhs==rhs は lhs\[Equal]rhs または lhsrhs という形で入力できる．
  • \[LongEqual]あるいは lhsrhs としても入力できる．
  • TraditionalFormでは，lhs==rhs は lhsrhs として出力される．

予備知識

  • Equal[expr1,expr2]は，expr1と expr2が数値的に等しい場合にTrueを，両者が等しくはなく等価性が立証されなかったために未評価となった場合にはFalseを返す．例えば，Equal[(1+Sqrt[5])/2,GoldenRatio]はTrue，Equal[1,2]はFalseを返し，Equal[1,a]は未評価で返される．Equal[expr1,expr2]は等号を使って expr1==expr2のように入力することも\[Equal]記号を使って expr1expr2のように入力することもできる．Equal[expr1,expr2,…]のように引数が複数の形（expr1==expr2…で入力可）は，式 expriすべてが数値的に等しい場合にはTrueを，少なくとも2つが異なる場合にはFalseを返し，それ以外の場合には未評価で返される．1引数形式のEqual[expr]は（少々逆説的ではあるが1引数形式のUnequal[expr])と同じように）Trueを返す．
  • 機械精度(MachinePrecision)以上の数は，たとえ二進表記で末尾7桁まで異なっていても等しいとみなされる．機械精度未満の数の等価性は，最低精度の数の精度内での一致に基づいて立証される．例えば，1.01`2==1はTrueを返すが1.01`3==1はFalseを返す．厳密な数量については，Equalは数値近似を使って等価性を立証するが，これは大域変数$MaxExtraPrecisionの値の影響を受ける．
  • Equalは数多くの他のシンボルと関連がある．「1個の等号」シンタックス expr1=expr2で入力できるSet[expr1,expr2]は expr2を評価してその結果が expr1の値になるような割当てを行うのに対し，「3個の等号」シンタックス expr1===expr2で入力可能なSameQ[expr1,expr2]は，expr1と expr2が等しい場合にはTrueを返しそれ以外の場合にはFalseを返す．SameQはEqualとは異なり，数の異なる表現形を区別する．例えば，SameQ[1,1.]とSameQ[1.,1.+0.I]はどちらもFalseを返す．SameQの動作は，SameQが常に評価結果としてTrueまたはFalseを返すのに対しEqualは等価性が立証できない場合には未評価のままである点でEqualのそれとも異なる．expr1!=expr2と入力できるUnequalはEqualの逆関数である．Equalには演算子形のEqualToもある．ブール論理で使われるEqualの類似関数はEquivalentである．
  • Equalが未評価で返されるケースについて，PossibleZeroQを使って問題の式が値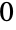を持つことがあるかどうかを示すことができる．例えば，Equal[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0]は評価されて返されるが，その第1引数に対してPossibleZeroQを呼ぶとTrueが（0という値が正確に実証されたものではないと言う有益なメッセージとともに）返される．Simplify，FullSimplify，RootReduce等の記号を簡約する関数もまた，（ここに挙げた例を含め）Equalには不可能な等価性の正確な証明に使われることがある．

例題

すべて開くすべて閉じる

例  (2)

等しいかどうかテストする：

方程式を表す：

スコープ  (12)

数値的等価性  (6)

数の等価性をテストする：

二進法で最高で最後の7桁が異なる近似数は等しいとみなされる：

厳密数の式と近似数を比較する：

2つの厳密数の式を比較する．等価ではないことの証明には数値テストで十分なことがある：

等価性の証明には記号的なメソッドが必要である：

Equalが使う記号メソッドでは，この等価性の証明には不十分である：

RootReduceを使って2つの代数的数が等しいかどうか判断する：

Equalが使う数値メソッドはこの式が等価ではないと証明するのに十分な精度ではない：

RootReduceは2つの代数的数が等価ではないことを証明する：

$MaxExtraPrecisionの値を大きくすることでも等価ではないことの証明ができるかもしれない：

記号的等価性  (6)

記号的な恒等式：

Equalは，自動的にはこの恒等式を証明しない：

Expandを使ってこれを証明する：

記号方程式：

Solveを使ってこの方程式を解く：

Reduceはパラメータの一般的ではない値を必要とするものを含めすべての解を返す：

3つ以上の式を比べる：

リストを比べる：

文字列を比べる：

特性と関係  (6)

2つの引数を持つEqualの否定はUnequalである：

3つの引数を持つEqualの否定は自動的には簡約されない：

LogicalExpandを使って2引数のUnequalについて上記を表現する：

3引数のEqualの否定は3引数のUnequalと等価ではない：

Equalは式で表されるオブジェクトの数学的等価性をテストする：

SameQは式の構文的等価性をテストする：

Equalが2つの数による式が等価かどうか判断できない場合は，未評価のまま返す：

FullSimplifyは厳密な記号的変換を使って等価性を証明する：

PossibleZeroQは数値的および記号的ヒューリスティックを使って式が零かどうか判断する：

PossibleZeroQが使う数値メソッドは数が零であると不正確に判断することがある：

Solveを使ってパラメータの一般的な値の方程式を解く：

Reduceは一般的ではないパラメータ値を使うものを含むすべての解を与える：

Reduceを使って指定の領域上で方程式を解く：

考えられる問題  (5)

機械精度の近似数の等価性は微妙なことがある：

余分な桁が等性を乱す：

任意精度の近似数にはこの問題はない：

自動精度追跡機能により，Equalには最初の10桁のみを見ればよいことが分かっている：

この場合は，機械数の等性テストが成功する：

この場合の余分な桁はEqualによって無視される：

等性は近似数にとっては推移的ではないことがある：

Equalは，ブールの等価演算子としては扱われない：

代りにEquivalentを使う：

Wolfram Research (1988), Equal, Wolfram言語関数， https://reference.wolfram.com/language/ref/Equal.html （2007年に更新）.

テキスト

Wolfram Research (1988), Equal, Wolfram言語関数， https://reference.wolfram.com/language/ref/Equal.html （2007年に更新）.

CMS

Wolfram Language. 1988. "Equal." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Equal.html.

APA

Wolfram Language. (1988). Equal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Equal.html

BibTeX

@misc{reference.wolfram_2024_equal, author="Wolfram Research", title="{Equal}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Equal.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_equal, organization={Wolfram Research}, title={Equal}, year={2007}, url={https://reference.wolfram.com/language/ref/Equal.html}, note=[Accessed: 21-November-2024 ]}