EulerMatrix[{α,β,γ}]
現行の ![]() 軸の周りで α 分回転させ,次に現行の
軸の周りで α 分回転させ,次に現行の ![]() 軸の周りで β 分回転させ,次に現行の
軸の周りで β 分回転させ,次に現行の ![]() 軸の周りで γ 分回転させることで形成される3Dオイラー回転行列を与える.
軸の周りで γ 分回転させることで形成される3Dオイラー回転行列を与える.
EulerMatrix[{α,β,γ},{a,b,c}]
最初に現行の a 軸の周りで α 分回転させ,次に現行の b 軸の周りで β 分,次に現行の c 軸の周りで γ 分回転させることに相当する3Dオイラー回転行列を与える.


EulerMatrix
EulerMatrix[{α,β,γ}]
現行の ![]() 軸の周りで α 分回転させ,次に現行の
軸の周りで α 分回転させ,次に現行の ![]() 軸の周りで β 分回転させ,次に現行の
軸の周りで β 分回転させ,次に現行の ![]() 軸の周りで γ 分回転させることで形成される3Dオイラー回転行列を与える.
軸の周りで γ 分回転させることで形成される3Dオイラー回転行列を与える.
EulerMatrix[{α,β,γ},{a,b,c}]
最初に現行の a 軸の周りで α 分回転させ,次に現行の b 軸の周りで β 分,次に現行の c 軸の周りで γ 分回転させることに相当する3Dオイラー回転行列を与える.
詳細とオプション




- EulerMatrixは,オイラー回転行列あるいはオイラー回転としても知られており,角 α,β,γ はしばしばオイラー角として言及される.
- EulerMatrixは,各回転が現行のあるいは固有座標フレームに言及している座標軸の周りの基本回転の連続として回転を指定する際によく使われる.
- EulerMatrix[{α,β,γ}]はEulerMatrix[{α,β,γ},{3,2,3}]に等しい.
- デフォルトの z-y-z 回転EulerMatrix[{α,β,γ},{3,2,3}]
- EulerMatrix[{α,β,γ},{a,b,c}]は,Rα,a=RotationMatrix[α,UnitVector[3,a]]等である
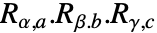 に等しい. »
に等しい. » - x-y-z 回転EulerMatrix[{α,β,γ},{1,2,3}]
- 回転軸 a,b,c は任意の整数1,2あるいは3でよい.しかし,任意の3D回転を指定するために十分一般的である組合せは12しかない.
- 最初と最後の軸が繰り返されている回転
-
{3,2,3} z-y-z 回転(デフォルト) 


{3,1,3} z-x-z 回転 

{2,3,2} y-z-y 回転 


{2,1,2} y-x-y 回転 


{1,3,1} x-z-x 回転 

{1,2,1} x-y-x 回転 

- 3軸すべてが異なる回転
-
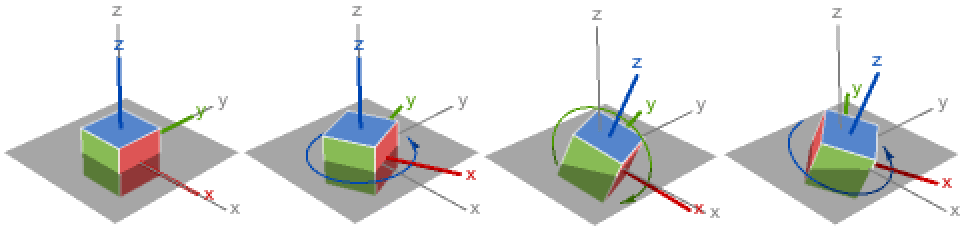
{1,2,3} x-y-z 回転 

{1,3,2} x-z-y 回転 

{2,1,3} y-x-z 回転 


{2,3,1} y-z-x 回転 


{3,1,2} z-x-y 回転 


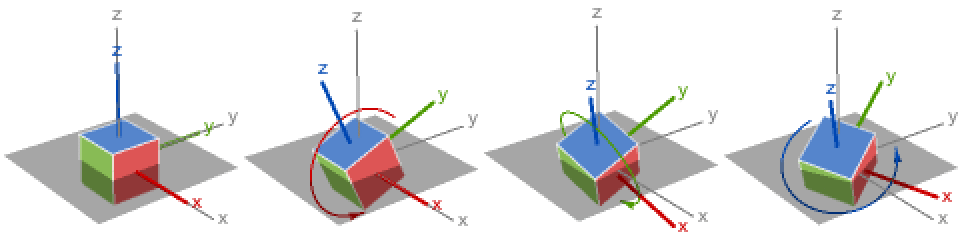
{3,2,1} z-y-x 回転 


- 続く軸が繰り返される回転も回転行列を作成するが,EulerAnglesを使って一意的に反転することはできない.
- EulerMatrixは,返す行列の構造を指定するオプションTargetStructureをサポートする.次は,TargetStructureの可能な設定である.
-
Automatic 返す表現を自動選択する "Dense" 行列を密な行列として表す "Orthogonal" 行列を直交行列として表す "Unitary" 行列をユニタリ行列として表す - EulerMatrix[…,TargetStructureAutomatic]はEulerMatrix[…,TargetStructure"Dense"]に等しい.
例題
すべて開く すべて閉じるスコープ (6)
GeometricTransformationを使って3Dでグラフィックスのプリミティブを回転させる:
TransformedRegionを使って領域を回転させる:
ImageTransformationを使って3D画像を回転させる:
アプリケーション (6)
図解 (1)
ジンバル (5)
ジンバルとは,オブジェクトそれ自体が任意の方向を向くことを許すピボットリングの系である.これは,さまざまなナビや画像アプリに使用されている:
ジンバル内のオブジェクトの向きは,最も外側のリングから最も内側のリングまでのリングの回転の角度とEulerMatrixを使ってモデル化することができる.a-b-a 軸の系が使われることに注意:
a-b-c 軸の回転のあるジンバルは,すべてのリングの軸がお互いに垂直である初期状態のジンバルの系をモデル化する:
回転系は,ある角度の値が系の自由度を減ずるジンバルロックに陥ちいることがある.通常の,このロックが起こらないケースでは以下が生成される:
ベクトル{1,1,0}は曲面上の任意の点で回転させることができる:
軸が ![]() のとき,ジンバルロックは
のとき,ジンバルロックは ![]() のときに起こる.次は x-y-x 回転の例である:
のときに起こる.次は x-y-x 回転の例である:
これはロックされていない m1とロックされた m2のケースである:
z-y-z 回転についての,アンロックされた m1とロックされた m2のケース:
特性と関係 (11)
EulerMatrixは3回転に相当する:
EulerAnglesを使って同じ回転行列を与える角度を返す:
各ステップで大域的座標フレームに関しての回転にRollPitchYawMatrixを使う:
EulerMatrixは現行の座標フレームに関して各ステップで回転する:
連続する2つの回転軸が等しいとき,つまり,![]() あるいは
あるいは ![]() であるとき,その系の自由度は x-y-y 回転を行うときのように2度である:
であるとき,その系の自由度は x-y-y 回転を行うときのように2度である:
すべての回転軸が等しいとき,つまり,![]() のとき,その系の自由度は x-x-x 回転を行うときのように1度である:
のとき,その系の自由度は x-x-x 回転を行うときのように1度である:
EulerMatrix[{α,β,γ},{a,b,c}]はRollPitchYawMatrix[{γ,β,α},{c,b,a}]と同じである:
EulerMatrixは![]() でのみ適用される:
でのみ適用される:
一般的な次元では,RotationMatrixを使う:
EulerMatrixは任意の回転を3軸配向回転についてパラメータ化する:
一般的な軸の周りの回転については,RotationMatrixを使う:
EulerMatrixは行列式1に関して直交行列である:
EulerMatrixの逆はその転置である:
EulerMatrix[{α,β,γ}]の逆はEulerMatrix[{-γ,-β,-α}]である:
EulerMatrix[{α,β,γ},{a,b,c}]の逆はEulerMatrix[{-γ,-β,-α},{c,b,a}]である:
考えられる問題 (1)
おもしろい例題 (1)
GeometricTransformationを使って,角度の範囲で球の回転を可視化する:
関連項目
EulerAngles RollPitchYawMatrix RollPitchYawAngles RotationMatrix RotationTransform OrthogonalMatrix UnitaryMatrix AnglePath3D
Function Repository: WignerMatrix
テキスト
Wolfram Research (2015), EulerMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/EulerMatrix.html (2024年に更新).
CMS
Wolfram Language. 2015. "EulerMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/EulerMatrix.html.
APA
Wolfram Language. (2015). EulerMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerMatrix.html
BibTeX
@misc{reference.wolfram_2025_eulermatrix, author="Wolfram Research", title="{EulerMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/EulerMatrix.html}", note=[Accessed: 10-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_eulermatrix, organization={Wolfram Research}, title={EulerMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/EulerMatrix.html}, note=[Accessed: 10-February-2026]}