FiniteFieldEmbedding
FiniteFieldEmbedding[ff1,ff2]
有限体 ff2における有限体 ff1の埋込みを与える.
FiniteFieldEmbedding[e1e2]
e1を e2に写像する周辺体 e2における周辺体 e1の埋込みを表す.
詳細

- 有限体の埋込みはガロア(Galois)体の埋込みまたは有限体単射としても知られている.
- 有限体の埋込みは,ある有限体を他の有限体の部分体と識別するためによく使われる.
- ℰ=FiniteFieldEmbedding[e1e2](ただし e1∈ff1かつ e2∈ff2)なら,
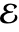 は ff1を ff2に写像する.
は ff1を ff2に写像する.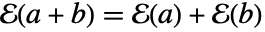 かつすべての
かつすべての 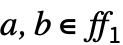 について
について 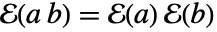 .
. - 有限体 ff1が ff2と同じ標数でありその拡大次数が ff2の拡大次数を割れるなら,ff1は ff2に埋め込める.
- 有限体の元 e1∈ff1と e2∈ff2は,両者が同じMinimalPolynomialを持ち e1が ff1を生成するときかつそのときに限って ff1の ff2への体の埋込みを定義する.2番目の条件は e1の最小多項式の次数が
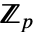 上の ff1の拡大次数と等しいときかつそのときに限って満足される.
上の ff1の拡大次数と等しいときかつそのときに限って満足される. - 埋込み ℰ=FiniteFieldEmbedding[e1e2]について, ℰ["Projection"]は
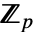 上のベクトル空間として扱われる,すべての
上のベクトル空間として扱われる,すべての 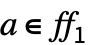 について
について 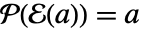 である e2の周辺体 ff2から e1の周辺体 ff1への線形写像
である e2の周辺体 ff2から e1の周辺体 ff1への線形写像 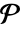 を表す.
を表す.
例題
すべて開くすべて閉じるスコープ (3)
アプリケーション (1)
Extensionオプションを使って最後の2つのステップを結合する:
特性と関係 (4)
ℰ["Projection"]は ![]() 線形写像であるが,乗算は保持しない:
線形写像であるが,乗算は保持しない:
ℰ["Projection"]と ![]() の合成は
の合成は ![]() の恒等式である:
の恒等式である:
有限体の自己同型はすべてフロベニウス自己同型の関数乗である:
ここでは aut[a]==FrobeniusAutomorphism[a,4]:
FiniteFieldElementTraceを使って![]() を計算する:
を計算する:
FiniteFieldElementNormを使って ![]() を計算する:
を計算する:
MinimalPolynomialを使って ![]() 上の
上の ![]() の元の最小多項式を求める:
の元の最小多項式を求める:
Compositionを使って有限体の埋込みを構成する:
テキスト
Wolfram Research (2023), FiniteFieldEmbedding, Wolfram言語関数, https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.
CMS
Wolfram Language. 2023. "FiniteFieldEmbedding." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.
APA
Wolfram Language. (2023). FiniteFieldEmbedding. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html
