WOLFRAM

Wolfram 语言与系统参考资料中心

FiniteFieldEmbedding[ff1,ff2]

给出有限域 ff1 在有限域 ff2 中的嵌入.

FiniteFieldEmbedding[e1e2]

表示 e1 的环境域在 e2 的环境域中的嵌入，它将 e1 映射到 e2.

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
应用  
属性和关系  
参见
相关指南
历史
按以下格式引用：

FiniteFieldEmbedding

FiniteFieldEmbedding[ff1,ff2]

给出有限域 ff1 在有限域 ff2 中的嵌入.

FiniteFieldEmbedding[e1e2]

表示 e1 的环境域在 e2 的环境域中的嵌入，它将 e1 映射到 e2.

更多信息

  • 有限域嵌入也称为伽罗瓦域嵌入或有限域单态.
  • 有限域嵌入通常用于识别一个有限域与另一个有限域的子域.
  • 如果 ℰ=FiniteFieldEmbedding[e1e2]，其中 e1∈ff1 且 e2∈ff2，则 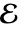将 ff1 映射至 ff2，并且对于所有 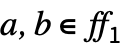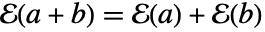a,b in ff_1，，且 .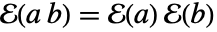
  • 如果有限域 ff1 与 ff2 具有相同的特征，并且它的扩张度是 ff2 的扩张度的除数，则有限域 ff1 可以嵌入到 ff2 中.
  • 当且仅当它们具有相同的 MinimalPolynomial 并且 e1 生成 ff1 时，有限域元素 e1∈ff1 和 e2∈ff2 定义 ff1 在 ff2 中的域嵌入. 后一个条件当且仅当 e1 的最小多项式次数等于 ff1 在 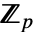上的扩张度时成立.
  • 对于嵌入 ℰ=FiniteFieldEmbedding[e1e2]，ℰ["Projection"] 表示从 e2 的环境场 ff2 到 e1 的环境场 ff1 的线性映射 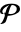，被视为 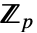上的向量空间，对于所有 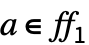a in ff_1，使得 .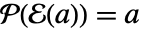

范例

打开所有单元 关闭所有单元

基本范例  (1)

表示具有特征 17 和扩张度 和 的有限域 和 ：

Wolfram Language code: {𝒦, ℱ} = {FiniteField[17, 3], FiniteField[17, 6]}

求 在 中的嵌入：

Wolfram Language code: ℰ = FiniteFieldEmbedding[𝒦, ℱ]

通过嵌入映射 的一个元素：

Wolfram Language code: ℰ[𝒦[123]]

将结果投影回 ：

Wolfram Language code: ℰ["Projection"][%]

范围  (3)

表示具有特征 和扩张度 和 的有限域 和 ：

Wolfram Language code: {𝒦, ℱ} = {FiniteField[29, 4], FiniteField[29, 12]}

求 在 中的嵌入：

Wolfram Language code: ℰ = FiniteFieldEmbedding[𝒦, ℱ]

域嵌入保留加法和乘法：

Wolfram Language code: {a, b} = {𝒦[123], 𝒦[456]}
Wolfram Language code: ℰ[a + b] == ℰ[a] + ℰ[b]
Wolfram Language code: ℰ[a b] == ℰ[a]ℰ[b]

ℰ["Projection"] 是 -线性映射但不保留乘法：

Wolfram Language code: {c, d} = {ℱ[123], ℱ[456]}
Wolfram Language code: ℰ["Projection"][2c + 3d] == 2ℰ["Projection"][c] + 3ℰ["Projection"][d]
Wolfram Language code: ℰ["Projection"][c d] == ℰ["Projection"][c]ℰ["Projection"][d]

ℰ["Projection"] 与 的组合是 上的恒等式：

Wolfram Language code: ℰ["Projection"][ℰ[a]] == a

反向组合不是 上的恒等式：

Wolfram Language code: ℰ[ℰ["Projection"][c]] == c

通过手动选择生成器及其值来指定域嵌入：

Wolfram Language code: {𝒦, ℱ} = {FiniteField[97, 4], FiniteField[97, 8]}; a = 𝒦[123]

如果 a 的最小多项式的次数等于 的扩张度，则生成 ：

Wolfram Language code: f = MinimalPolynomial[a, x]

求 f 在 中的根：

Wolfram Language code: Factor[f, Extension -> ℱ]

选择其中一个根：

Wolfram Language code: b = -FiniteFieldElement[FiniteField[97, 5 + 32*#1 + #1^2 + 65*#1^3 + #1^8 & , "Polynomial"], {19, 90, 24, 20, 11, 95, 91, 9}]

表示 在 中的嵌入，将 a 映射到 b：

Wolfram Language code: ℰ = FiniteFieldEmbedding[a -> b]

为使得嵌入存在，两个域需要具有相同的特征：

Wolfram Language code: FiniteFieldEmbedding[FiniteField[2, 3], FiniteField[3, 6]]

第一个域的扩张度需要是第二个域的扩张度的除数：

Wolfram Language code: FiniteFieldEmbedding[FiniteField[2, 4], FiniteField[2, 6]]

应用  (1)

在有限域的代数扩张中对多项式进行因式分解：

Wolfram Language code: 𝒦 = FiniteField[59, 3]; f = 𝒦[123]x ^ 2 + 𝒦[234]x + 𝒦[345]
Wolfram Language code: IrreduciblePolynomialQ[f]

将 嵌入到具有 个元素的有限域中：

Wolfram Language code: ℱ = FiniteField[59, 6]; ℰ = FiniteFieldEmbedding[𝒦, ℱ]

通过嵌入映射 f：

Wolfram Language code: ff = f /. a_FiniteFieldElement :> ℰ[a]

对结果进行因式分解：

Wolfram Language code: Factor[ff]

使用 Extension 选项合并最后两个步骤：

Wolfram Language code: Factor[f, Extension -> ℰ]

属性和关系  (4)

域嵌入保留加法和乘法：

Wolfram Language code: {𝒦, ℱ} = {FiniteField[7, 3], FiniteField[7, 9]}; ℰ = FiniteFieldEmbedding[𝒦, ℱ];
Wolfram Language code: {a, b} = {𝒦[123], 𝒦[456]}
Wolfram Language code: ℰ[a + b] == ℰ[a] + ℰ[b]
Wolfram Language code: ℰ[a b] == ℰ[a]ℰ[b]

ℰ["Projection"] 是 -线性映射但不保留乘法：

Wolfram Language code: {c, d} = {ℱ[123], ℱ[456]}
Wolfram Language code: ℰ["Projection"][2c + 3d] == 2ℰ["Projection"][c] + 3ℰ["Projection"][d]
Wolfram Language code: ℰ["Projection"][c d] == ℰ["Projection"][c]ℰ["Projection"][d]

ℰ["Projection"] 与 的组合是 上的恒等式：

Wolfram Language code: ℰ["Projection"][ℰ[a]] == a

反向组合不是 上的恒等式：

Wolfram Language code: ℰ[ℰ["Projection"][c]] == c

求 的自同构：

Wolfram Language code: ℱ = FiniteField[71, 5]; aut = FiniteFieldEmbedding[ℱ, ℱ]

所有有限域自同构都是弗罗贝尼乌斯自同构的功能幂（Functional Power）：

Wolfram Language code: Table[FrobeniusAutomorphism[ℱ[71], k], {k, 4}]

这里 aut[a]==FrobeniusAutomorphism[a,4]：

Wolfram Language code: aut[ℱ[1234]] == FrobeniusAutomorphism[ℱ[1234], 4]

嵌入允许用 的子域识别 ：

Wolfram Language code: {𝒦, ℱ} = {FiniteField[43, 3], FiniteField[43, 6]}; ℰ = FiniteFieldEmbedding[𝒦, ℱ]

使用 FiniteFieldElementTrace 计算 ：

Wolfram Language code: FiniteFieldElementTrace[ℱ[123], ℰ]

使用 FiniteFieldElementNorm 计算 ：

Wolfram Language code: FiniteFieldElementNorm[ℱ[123], ℰ]

使用 MinimalPolynomial 在 上求 的元素的最小多项式：

Wolfram Language code: MinimalPolynomial[ℱ[123], x, ℰ]

使用 Composition 组成有限域嵌入：

Wolfram Language code: 𝒦 = FiniteField[71, 3]; ℱ = FiniteField[71, 6]; 𝒢 = FiniteField[71, 12]; Subscript[ℰ, 1] = FiniteFieldEmbedding[𝒦, ℱ]; Subscript[ℰ, 2] = FiniteFieldEmbedding[ℱ, 𝒢]; Subscript[ℰ, 21] = Subscript[ℰ, 2] @* Subscript[ℰ, 1]
Wolfram Language code: Subscript[ℰ, 21][𝒦[123]] == Subscript[ℰ, 2][Subscript[ℰ, 1][𝒦[123]]]
Wolfram Research (2023)，FiniteFieldEmbedding，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.

文本

Wolfram Research (2023)，FiniteFieldEmbedding，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.

CMS

Wolfram 语言. 2023. "FiniteFieldEmbedding." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.

APA

Wolfram 语言. (2023). FiniteFieldEmbedding. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html 年

BibTeX

@misc{reference.wolfram_2026_finitefieldembedding, author="Wolfram Research", title="{FiniteFieldEmbedding}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_finitefieldembedding, organization={Wolfram Research}, title={FiniteFieldEmbedding}, year={2023}, url={https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html}, note=[Accessed: 03-November-2026]}