FractionalD
FractionalD[f,{x,α}]
给出函数 f 的 α 阶黎曼–刘维尔分数导数 ![]() .
.
更多信息和选项

- FractionalD 也称为 f 的黎曼–刘维尔微分积分.
- FractionalD 将 D 推广到分数阶,并统一了微积分的导数和积分的概念.
- FractionalD 在分数微积分中起着基础作用,因为可以根据它定义其他类型的分数导数,例如 CaputoD.
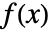 的
的 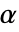 阶黎曼–刘维尔分数导数由
阶黎曼–刘维尔分数导数由 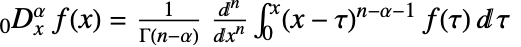 定义,其中
定义,其中 ![n=max(0,TemplateBox[{alpha}, Ceiling]) n=max(0,TemplateBox[{alpha}, Ceiling])](Files/FractionalD.zh/5.png) .
. - 分数阶导数在整数阶导数之间“插值”,如下所示,对于函数
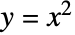 及其
及其 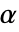 阶分数导数由
阶分数导数由 ![2/TemplateBox[{{3, -, alpha}}, Gamma] x^(2-alpha) 2/TemplateBox[{{3, -, alpha}}, Gamma] x^(2-alpha)](Files/FractionalD.zh/8.png) 给出,其中
给出,其中 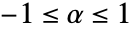 :
: - 分数导数的阶 α 可以是符号数或任意实数.
- FractionalD[array,{x,α}] 将 FractionalD 线性作用于 array 的各个元素.
- FractionalD 对输入函数的参数采取不同的 Assumptions.
- 所有不显式依赖给定变量
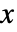 的表达式都被解释为常量.
的表达式都被解释为常量.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (8)
Exp 函数关于 x 的 0.23-阶分数导数:
对于负整数 ![]() ,FractionalD 与普通不定积分相差一个常数:
,FractionalD 与普通不定积分相差一个常数:
Sin 函数的分数导数用 HypergeometricPFQ 的形式写成:
BesselJ 函数的分数导数:
MeijerG 函数的分数导数以另一个 MeijerG 函数的形式给出:
将 LaplaceTransform 应用于 Exp 的 FractionalD 得到相同的结果:
选项 (1)
Assumptions (1)
FractionalD 可能返回 ConditionalExpression:
使用 Assumptions 限制参数将简化输出:
属性和关系 (6)
FractionalD 对所有实数 ![]() 有定义:
有定义:
FractionalD 对于复阶数 ![]() 没有定义:
没有定义:
FractionalD 结果可能包含 DifferenceRoot 序列:
如果 ![]() 是给定的实数,则此一般表达式被简化为 HypergeometricPFQ 实例的有限和:
是给定的实数,则此一般表达式被简化为 HypergeometricPFQ 实例的有限和:
使用 NFractionalD 函数可以更快地进行数值计算:
文本
Wolfram Research (2022),FractionalD,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FractionalD.html.
CMS
Wolfram 语言. 2022. "FractionalD." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FractionalD.html.
APA
Wolfram 语言. (2022). FractionalD. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FractionalD.html 年