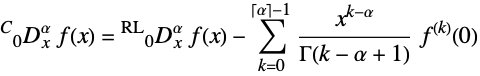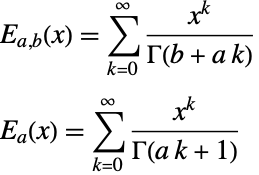Fractional Calculus
Introduction
Fractional calculus develops the theory of differentiation and integration of any real or complex order. It extends the classical calculus basic operations to fractional orders and studies the methods of solving differential equations involving these fractional-order derivatives and integrals [1].
Fractional calculus is not just a pure mathematical theory. This branch is becoming more and more popular in diffusion problems, fluid dynamics, control theory, signal processing and other areas. A lot of scientific phenomena are described with fractional differential, integral and mixed-type equations. So realizing the importance and potential of this topic, functions have been developed for exploring the fractional calculus ecosystem in the Wolfram Language.
In a few words: Fractional calculus is able to generalize any integral or differential equation into an infinite set of its "fractional" analogs (where fractional-order integrals and derivatives are involved). So it extends our possibilities to describe a new set of physical phenomena and improve the accuracy of already-existing models.
Brief History of Fractional Calculus
The foundations of calculus were developed by Newton and Leibniz in the seventeenth century, with differentiation and integration of integer order being the two fundamental operations of this subject.
In 1695, Leibniz wrote about the meaning of the half-order derivative in his message to L’Hôpital. An impulse to this fractional-order calculus theory was given by Niels Abel, who wrote two articles in 1823 and 1826 where all the elements of the theory can be found: the idea of fractional-order integration and differentiation, the mutually inverse relationship between them and the understanding that fractional-order differentiation and integration can be considered as the same generalized operation and so on.
Abel considered the generalized version of the tautochrone problem (also known as Abel's problem), where the integral equation ![]() was solved for the given transit time function
was solved for the given transit time function ![]() as a function from the distance
as a function from the distance ![]() . The determination of the unknown function
. The determination of the unknown function ![]() makes it possible to find the equation for the tautochrone curve itself.
makes it possible to find the equation for the tautochrone curve itself.
After several algebraic manipulations, this integral equation can be rewritten in the form ![]() , which is what is now called the half-order Caputo fractional derivative [2].
, which is what is now called the half-order Caputo fractional derivative [2].
Until the second half of the twentieth century, the fractional calculus was mainly developed as an abstract mathematical theory. It gained a lot of practical applications during the last few decades as scientists from different areas and backgrounds worked on this theory, considering it and its applications from different points of view. Hence, there are different approaches on how to define a fractional “differintegration” operation, but three of these are the most popular.
What Is Fractional Calculus?
Integration is essentially the inverse operation of differentiation, hence it is possible to define one united operation of differentiation/integration, the so-called differintegral: in the literature, this operator is written as ![]() . Here the order of differentiation/integration is given by the parameter
. Here the order of differentiation/integration is given by the parameter ![]() , which in theory can be any real or complex number. If it is a positive integer, then it reduces to the ordinary differentiation; if it is negative integer, then it reduces to the ordinary integration.
, which in theory can be any real or complex number. If it is a positive integer, then it reduces to the ordinary differentiation; if it is negative integer, then it reduces to the ordinary integration.
Also, the fractional differintegrals depend on the value of the function ![]() at point
at point ![]() (the lower bound): it is an additional parameter describing the “history” of the function. In practice, the lower bound is usually taken to be 0 so that fractional-order derivatives/integrals include the values of the function at the origin; this is useful for the solutions of initial value problems.
(the lower bound): it is an additional parameter describing the “history” of the function. In practice, the lower bound is usually taken to be 0 so that fractional-order derivatives/integrals include the values of the function at the origin; this is useful for the solutions of initial value problems.
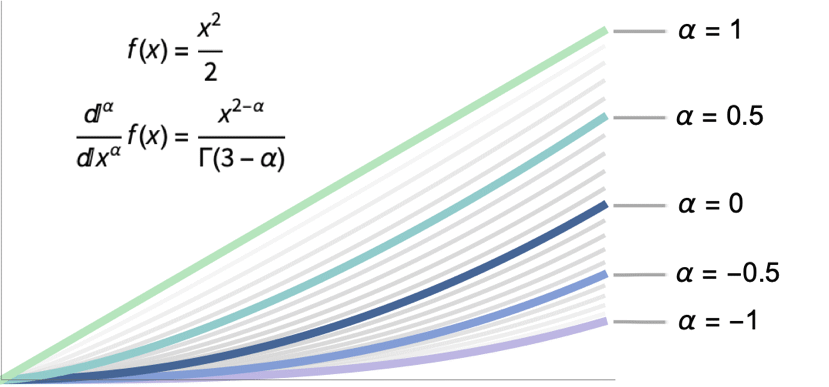
The most important starting point for the fractional calculus theory is that irrespective of the definition of fractional differintegration operator, it should coincide with the ordinary differentiation/integration operators for integer ![]() 's. In the following illustration, the plots of a square function and its ordinary and fractional-order derivatives and integrals are shown:
's. In the following illustration, the plots of a square function and its ordinary and fractional-order derivatives and integrals are shown:
The Fractional-Order Derivatives of the Square Function
It is well known that the first derivative of the square function ![]() is
is ![]() and the integral of it is
and the integral of it is ![]() , but what is the half-order derivative of this function? Or the opposite operation, integral of the function?
, but what is the half-order derivative of this function? Or the opposite operation, integral of the function?
Take a look at the formula of the ![]() th-order ordinary derivative of the square function:
th-order ordinary derivative of the square function:
Putting negative ![]() in this formula, one might easily get the
in this formula, one might easily get the ![]() th-order antiderivative of this function:
th-order antiderivative of this function:
Nothing stops one from taking the same formula and substituting some noninteger order ![]() into it:
into it:
Now, taking the ![]() th-order ordinary derivative of the latter function and substituting
th-order ordinary derivative of the latter function and substituting ![]() into it, one arrives at the following:
into it, one arrives at the following:
Obviously, this is the first derivative of the square function obtained via two "half-order fractional differentiation" procedures. Moreover, one might easily verify that the antiderivative of the square function can be obtained via two similar half-order integration procedures (substituting ![]() in the previously shown formulas). The above shown manipulations are nothing other than the fractional-order differintegration of a square function.
in the previously shown formulas). The above shown manipulations are nothing other than the fractional-order differintegration of a square function.
Definitions of Fractional Differintegrals
1. Grünwald–Letnikov approach . The Grünwald–Letnikov differintegral gives the obvious extension of the classical derivatives/integrals and is based on limits:
In practice, this approach is not very usable, as it contains an infinite number of approximations of a function at different points. There are different advanced algorithms for calculating it [3], but from a practical point of view they are computationally expensive.
2. Riemann–Liouville differintegral . The Riemann–Liouville definition is:
The Riemann–Liouville approach underlies a solid and strict mathematical theory of fractional calculus. This theory is well developed, but the Riemann–Liouville approach has a couple of limitations that make it not truly suitable for applications in real-world problems; however, it is very important for theoretical aspects.
3. Caputo differintegral . The Caputo definition is:
There is a similarity between this and Riemann–Liouville differintegrals. In fact, the Caputo differintegral can be defined via the Riemann–Liouville approach:
Based on the definition, the Caputo fractional derivatives coincide with the Riemann–Liouville fractional derivatives for negative orders ![]() .
.
The Caputo definition of differintegral has many advantages in comparison with the Riemann–Liouville or Grünwald–Letnikov definitions: first, it takes into consideration the values of the function and its derivatives at the origin (or, in general, at any lower-limit point ![]() ), which automatically makes it suitable for solving fractional-order initial-value problems using Laplace transforms. Also, the Caputo fractional derivative of a constant is 0 (while, in general, the Riemann–Liouville fractional derivative is not), hence it is more consistent with classical calculus.
), which automatically makes it suitable for solving fractional-order initial-value problems using Laplace transforms. Also, the Caputo fractional derivative of a constant is 0 (while, in general, the Riemann–Liouville fractional derivative is not), hence it is more consistent with classical calculus.
The following animation shows the behavior of the Caputo fractional derivatives of a square function in comparison with the ordinary ones—as one can see, the fractional-order derivatives interpolate between the integer orders and coincide with the ordinary derivatives for the integer orders of differintegration:
Fractional Differintegrals in the Wolfram Language
The Wolfram Language includes the FractionalD and CaputoD functions that stand for the Riemann-Liouville and Caputo fractional differintegrals [4-5], respectively. These functions compute the fractional derivatives ![]() and
and ![]() symbolically.
symbolically.
FractionalD Function
Here is a toy example showing how fractional derivative rules might be derived. The half-order fractional derivative of a cubic function is calculated using the Riemann–Liouville definition:
Repeating this once more, one will get the first order ordinary derivative:
The above input is just the direct application of the Riemann-Liouville definition of the fractional differintegral. Now verify this result using the built-in FractionalD function:
The following calculation recovers the initial function using three nested fractional integrations (ordinary integration is the same as three 1/3 order fractional integrations):
Now compute the arbitrary fractional-order derivative of this cubic function, make a table of specific orders and plot the list of derivatives:
Next, compute the 0.23-order fractional derivatives of the Exp and BesselJ functions:
The fractional derivatives of MeijerG are given in terms of another MeijerG function:
The above case is a very important theoretical feature and may be used for generation of FractionalD rules of complex functions through their MeijerG representation gained by another built-in MeijerGReduce function.
As a final example, a table of the ![]() th Riemann–Liouville fractional and
th Riemann–Liouville fractional and ![]() th ordinary derivatives for a few common special functions is presented:
th ordinary derivatives for a few common special functions is presented:
CaputoD Function
The CaputoD function gives the Caputo fractional derivative ![]() . This is a more useful function for real world applications as based on its theoretical definition it takes into consideration the values of the function at the origin.
. This is a more useful function for real world applications as based on its theoretical definition it takes into consideration the values of the function at the origin.
One basic important feature is that the Caputo fractional derivative of a constant is 0 (while the Riemann–Liouville derivative is not):
For negative orders of ![]() , the CaputoD output coincides with FractionalD—this is just because of their definitions:
, the CaputoD output coincides with FractionalD—this is just because of their definitions:
Now, compute the 0.23-order Caputo fractional derivative of the Exp function:
Compute the half-order Caputo fractional derivative of the BesselJ function:
And as a final example, the half-order Caputo fractional derivatives of some common mathematical functions are presented:
Numerical Fractional Differintegration
FractionalD and CaputoD are important and rather powerful functions but due to the complexity of their definitions (derivative of the integral or integral of the derivative of a function multiplied with other power function), calculations may be time consuming and they may generate cumbersome outputs. Or another scenario is that for wide classes of inputs, the built-in integration method is not able to generate any outputs. The following case shows an example where the FractionalD generates an output containing general holonomic sequences given by the DifferenceRoot function:
Having numerical analogs of such symbolic functions is profitable: for Integrate there is the numerical analog of it NIntegrate, DSolve has NDSolve, and so on. Similarly, FractionalD and CaputoD have the numerical analogs called the NFractionalD and NCaputoD functions, respectively, based on different algorithms presented in [1] and [3]. The design of these functions is simple—they simply generate a numerical output corresponding to the value of the fractional derivative of the given order at the given point. In the following example, the value of the half-order fractional derivative of the square function is calculated at the point ![]() :
:
Here a more complex case is presented:
Using these functions, one can gain insights into the behavior of the fractional derivative (for example, plotting it). As an example, consider the first output of this chapter having DifferenceRoot in the output. Generally speaking it is not known what functions are involved in the fractional derivative of the ![]() function. However, plotting this fractional derivative via the NFractionalD or NCaputoD function, one can gain some understanding:
function. However, plotting this fractional derivative via the NFractionalD or NCaputoD function, one can gain some understanding:
Here is another example involving the NCaputoD function:
Also, the Grünwald–Letnikov approach of fractional differentiation and integration is available in NFractionalD:
This, in fact, numerically corresponds with the Riemann–Liouville result:
Fractional Laplace Transforms
Laplace transforms and MittagLefflerE functions play a crucial role in solutions of differential equations containing fractional-order derivatives and integrals. Below, some basic information about MittagLefflerE is given and the methods of solving fractional-order differential equations (FDEs) via LaplaceTransform are also presented.
The MittagLefflerE function is the natural generalization of the exponential function: just as any ODE with constant coefficients is solved in exponential functions, so also any FDE with constant coefficients is solved in MittagLefflerE functions. Here are the definitions of ordinary and generalized MittagLefflerE functions:
The exponential function is a special case of MittagLefflerE:
Laplace transforms of the MittagLefflerE functions can be computed using the Wolfram Language:
LaplaceTransform converts a time-domain MittagLefflerE to frequency domain, also known as ![]() -domain:
-domain:
This frequency-domain function has poles and a branch cut going from negative infinity to the origin on the real axis:
Applying InverseLaplaceTransform, the initial Mittag–Leffler function is recovered:
A whole class of ![]() -domain functions is inverse Laplace transformed into
-domain functions is inverse Laplace transformed into ![]() -domain expressions containing Mittag–Leffler functions:
-domain expressions containing Mittag–Leffler functions:
One can recover the initial ![]() -domain function using LaplaceTransform:
-domain function using LaplaceTransform:
It is well known that the Laplace transform technique for integer order derivatives plays an important role for solving integer order differential equations. This is because, as an example, the LaplaceTransform of the second-order derivative can be expressed in terms of the function's LaplaceTransform:
A similar property holds for the LaplaceTransform of the fractional-order derivatives. For example, here is the LaplaceTransform of the 3/2-order CaputoD derivative:
Now one can use this property to calculate the Laplace transform of a Caputo derivative of, say, sine function:
The same result can be obtained if one first calculates the CaputoD of the sine function, then applies LaplaceTransform to the output:
The advantage of the first approach is that one only needs to calculate the LaplaceTransform of the Sin function, whereas in the second approach one has to find the LaplaceTransform of the more complicated HypergeometricPFQ function that arises in the CaputoD of Sin.
It is now natural to proceed to the next section about solving fractional differential equations.
Fractional Differential Equations
Fractional differential equations (FDEs) are differential equations involving fractional derivatives ![]() . These are generalizations of the ordinary differential equations (ODEs) that have attracted much attention and have been widely used in engineering, physics, chemistry, biology and other fields.
. These are generalizations of the ordinary differential equations (ODEs) that have attracted much attention and have been widely used in engineering, physics, chemistry, biology and other fields.
As a first step, linear fractional ODEs with constant coefficients are considered. As in the case of ODEs, one can use LaplaceTransform to transform the initial fractional differential equation to some algebraic equation in the ![]() -domain and solve it. Then the time-domain solution to the initial fractional differential equations using InverseLaplaceTransform is recovered. This process is demonstrated below.
-domain and solve it. Then the time-domain solution to the initial fractional differential equations using InverseLaplaceTransform is recovered. This process is demonstrated below.
First apply LaplaceTransform on both sides of the fractional differential equation with some initial values:
Then solve it for the LaplaceTransform:
And finally, apply InverseLaplaceTransform to find the time-domain solution:
Now, plot this time-domain function:
This solution can be directly derived using DSolve:
DSolve is able to solve any linear FDE with constant coefficients. Here is an example of a half-order FDE:
This solution may be verified as follows:
Here, solve a fractional integro-differential equation:
For Caputo-type FDEs, the initial conditions are to be given for integer order derivatives. The number of initial conditions depends on the order ![]() of FDE and is equal to
of FDE and is equal to ![]() . Below is the solution of an initial value problem for the previous example:
. Below is the solution of an initial value problem for the previous example:
Plot the solution to visualize the oscillatory behavior:
This example solves an FDE of order ![]() including four initial conditions:
including four initial conditions:
Here is the plot of the solution:
DSolve can also handle some linear systems of FDEs with constant coefficients. All equations in the system must have the same order ![]() . For example:
. For example:
Parametrically plot the solution:
And as a final example, here is the solution for a system of three FDEs using vector variables:
Applications
Recently fractional calculus has started to gain more and more applications in different areas of science. Here are some examples.
Fractional Harmonic Oscillator
The equation of the fractional harmonic oscillator of order 1.9 is:
The behavior of this fractional harmonic oscillator is very similar to the behavior of the ordinary damped harmonic oscillator:
Plot the fractional and damped harmonic oscillator solutions and compare them:
This example clearly demonstrates that the order of FDE can be used as a controlling parameter to model some complicated systems.
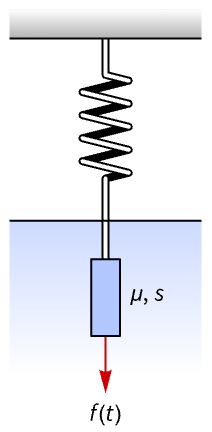
A Dynamical System with Fractional Damping
Consider a dynamical system consisting of a thin plate of mass ![]() and area
and area ![]() that is immersed in a Newtonian fluid of infinite extension with density
that is immersed in a Newtonian fluid of infinite extension with density ![]() and viscoelastic constant
and viscoelastic constant ![]() and is connected to a fixed point via a spring with spring constant
and is connected to a fixed point via a spring with spring constant ![]() . Suppose that the surface of the plate is sufficiently large so that the fluid slows the movement of the plate.
. Suppose that the surface of the plate is sufficiently large so that the fluid slows the movement of the plate.
This system can be modeled by a second-order differential equation with fractional damping, using parameters ![]() and
and ![]() [6]:
[6]:
Solve the model equation for step-like force ![]() with the parameter values
with the parameter values ![]() ,
, ![]() and plot the solution:
and plot the solution:
Fractional LC Circuit
This equation describes a fractional LC electrical circuit:
One could get the classical solution by specifying ![]() :
:
For ![]() , this gives the fractional generalized model, for which the solution is:
, this gives the fractional generalized model, for which the solution is:
Plot the solution for various values of equation order ![]() :
:
Fractional RC Circuit
One can also solve the equation of a fractional RC electrical circuit:
Here is the classical solution (![]() ):
):
The solution of the fractional generalized model (![]() ) is:
) is:
Plot the solution for various values of the order ![]() :
:
Fractional Wave Equation
Consider the following fractional wave equation:
DSolve is able to solve it:
Summary
Nowadays, fractional calculus is gaining more and more interest as it is able to generalize the well-known integro-differential equations to ones containing fractional-order derivatives or integrals of the target function—more general equations are able to more precisely describe different real-world phenomena.
In view of this potential, the Wolfram Language includes two basic operators for fractional calculus (the FractionalD and CaputoD functions). A huge effort has also been made to add support for solving fractional differential equations via DSolve with LaplaceTransform.
The Wolfram Language also includes numerical support for the fractional differintegration using NFractionalD and NCaputoD. NFractionalD has two internal methods standing for the Riemann–Liouville and Grünwald–Letnikov approaches, which should suffice for most practical applications.
References
1. Oldham, K. B. and J. Spanier. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Academic Press, 1974.
2. Podlubny, I., Magin, R. and I. Trymorush. "Niels Henrik Abel and the Birth of Fractional Calculus." Fractional Calculus and Applied Analysis 20, no. 5 (2017): pp. 1068–1075.
3. Li, C. and M. Cai. Theory and Numerical Approximations of Fractional Integrals and Derivatives. SIAM, 2019.
4. New in Wolfram Language 13.1 webinar series.
5. T. Ishkhanyan. "Fractional Calculus in Wolfram Language 13.1" blog post.
6. Kilbas A., Srivastava, H. M. and J. J. Trujillo. Theory and Applications of Fractional Differential Equations. Elsevier, 2006.