NFractionalD[f,{x,α},x0]
gives a numerical approximation to the Riemann–Liouville fractional derivative ![]() of order α of the function f at the point x0.
of order α of the function f at the point x0.


NFractionalD
NFractionalD[f,{x,α},x0]
gives a numerical approximation to the Riemann–Liouville fractional derivative ![]() of order α of the function f at the point x0.
of order α of the function f at the point x0.
Details and Options

- NFractionalD is the numerical analog of FractionalD, also known as the Riemann–Liouville differintegral of f.
- The Riemann–Liouville fractional derivative of
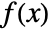 of order
of order 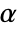 is defined as
is defined as 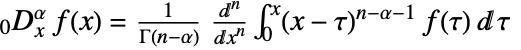 , where
, where ![n=max(0,TemplateBox[{alpha}, Ceiling]) n=max(0,TemplateBox[{alpha}, Ceiling])](Files/NFractionalD.en/5.png) .
. - NFractionalD is typically used in cases when symbolic evaluation with FractionalD fails.
- The following options can be given to NFractionalD:
-
Method Automatic method to use AccuracyGoal Infinity digits of absolute accuracy sought PrecisionGoal Automatic digits of precision sought WorkingPrecision MachinePrecision the precision used in internal computations - The following Method option settings may be used:
-
Automatic automatically selected method "GrunwaldLetnikov" Grünwald-Letnikov fractional differintegration scheme "RiemannLiouville" Riemann-Liouville fractional differintegration scheme
Examples
open all close allBasic Examples (4)
Scope (9)
Plot the ![]() -order fractional derivative of the square function with respect to x:
-order fractional derivative of the square function with respect to x:
Calculate the 0.23-order fractional derivative of the Exp function numerically and symbolically:
Calculate the value of the half-order derivative of the ArcTan function at some point:
The ![]() -order fractional derivative of the Sin function:
-order fractional derivative of the Sin function:
The ![]() -order fractional integral of the Sin function:
-order fractional integral of the Sin function:
The half-order fractional derivative of the AiryAi function:
Numerically calculate the fractional derivative of the BesselJ function:
Numerically calculate the fractional derivative of the MeijerG function:
Plot the numerically calculated fractional derivatives and integrals of a trigonometric product:
Options (2)
Method (2)
NFractionalD has two built-in methods, the Riemann–Liouville and the Grünwald–Letnikov methods:
If the Method is not specified, NFractionalD automatically uses the Riemann–Liouville approach:
In some cases, the Grünwald–Letnikov method is able to calculate the numerical fractional derivative:
It is not possible to calculate this fractional derivative using the Riemann–Liouville method:
Applications (3)
NFractionalD is able to numerically calculate fractional derivatives when FractionalD fails:
FractionalD outputs may contain DifferenceRoot sequences:
For a specific order of fractional differentiation, this is a cumbersome sum of HypergeometricPFQ functions:
However, the numerically calculated fractional derivative plot might be insightful:
Effectively generate a list of numerical values of fractional derivatives of a complex function using NFractionalD:
Properties & Relations (6)
NFractionalD is defined for all real ![]() :
:
In general, the fractional derivative of a constant is not 0:
NFractionalD gives the output in WorkingPrecision (if not specified, it is MachinePrecision):
If the Method option is not specified, NFractionalD uses the "RiemannLiouville" method:
Plot the fractional derivative using the numerical NFractionalD approach:
Compare with the symbolic FractionalD approach:
For negative orders ![]() , NCaputoD coincides with NFractionalD:
, NCaputoD coincides with NFractionalD:
Possible Issues (3)
NFractionalD will generate an error message if the Method option is not correct:
NFractionalD will generate an error message if the precision of input is less than the WorkingPrecision:
NFractionalD takes only numeric points of evaluation:
Neat Examples (2)
Plot the Sin function and its half, first and ![]() -order derivatives:
-order derivatives:
Numerical fractional derivative of MittagLefflerE at a point:
Generate a list of numerical values of the fractional derivative of the MittagLefflerE function:
See Also
FractionalD CaputoD NCaputoD D Integrate LaplaceTransform DSolve
Tech Notes
Related Guides
History
Text
Wolfram Research (2022), NFractionalD, Wolfram Language function, https://reference.wolfram.com/language/ref/NFractionalD.html.
CMS
Wolfram Language. 2022. "NFractionalD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NFractionalD.html.
APA
Wolfram Language. (2022). NFractionalD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NFractionalD.html
BibTeX
@misc{reference.wolfram_2025_nfractionald, author="Wolfram Research", title="{NFractionalD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/NFractionalD.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_nfractionald, organization={Wolfram Research}, title={NFractionalD}, year={2022}, url={https://reference.wolfram.com/language/ref/NFractionalD.html}, note=[Accessed: 06-January-2026]}