NCaputoD[f,{x,α},x0]
gives a numerical approximation to the Caputo fractional derivative ![]()
![]() of order α of the function f at the point x0.
of order α of the function f at the point x0.


NCaputoD
NCaputoD[f,{x,α},x0]
gives a numerical approximation to the Caputo fractional derivative ![]()
![]() of order α of the function f at the point x0.
of order α of the function f at the point x0.
Details and Options
- NCaputoD is the numerical analog of CaputoD, also known as the Caputo differintegral of f.
- The Caputo fractional derivative of order
 of
of 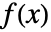 is defined as
is defined as 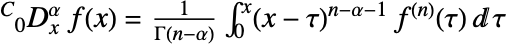 , where
, where ![n=max(0,TemplateBox[{alpha}, Ceiling]) n=max(0,TemplateBox[{alpha}, Ceiling])](Files/NCaputoD.en/6.png) .
. - NCaputoD is typically used in cases when symbolic evaluation with CaputoD fails.
- The following options can be given to NCaputoD:
-
AccuracyGoal Infinity digits of absolute accuracy sought PrecisionGoal Automatic digits of precision sought WorkingPrecision MachinePrecision the precision used in internal computations
Examples
open all close allBasic Examples (4)
Calculate the half-order Caputo fractional derivative of a quadratic function with respect to x at a point:
Plot the ![]() -order Caputo fractional derivative of an exponential function:
-order Caputo fractional derivative of an exponential function:
Numerical Caputo fractional derivative of MittagLefflerE at some point:
Generate a list of numerical values of the Caputo fractional derivative of the MittagLefflerE function:
Scope (8)
Plot the ![]() -order Caputo fractional derivative of the square function with respect to x:
-order Caputo fractional derivative of the square function with respect to x:
Calculate the 0.23-order Caputo fractional derivative of the Exp function numerically and symbolically:
Calculate the value of the half-order Caputo derivative of the ArcTan function at some point:
The ![]() -order Caputo fractional derivative of the Sin function:
-order Caputo fractional derivative of the Sin function:
The ![]() -order Caputo fractional integral of the Sin function:
-order Caputo fractional integral of the Sin function:
The half-order Caputo fractional derivative of the AiryAi function:
Numerically calculate the Caputo fractional derivative of the BesselJ function:
Plot the numerically calculated fractional derivatives and integrals of complex functions:
Applications (3)
NCaputoD is able to numerically calculate fractional derivatives when CaputoD fails:
CaputoD outputs might be cumbersome:
However, the plot of numerically calculated fractional derivative might be insightful:
Effectively generate a list of numerical values of Caputo fractional derivatives of a complex function using NCaputoD:
Properties & Relations (4)
NCaputoD is defined for all real ![]() :
:
The Caputo fractional derivative of a constant is 0:
Plot the Caputo fractional derivative using the numerical NCaputoD approach:
Compare with the symbolic CaputoD approach:
For negative orders ![]() , NCaputoD coincides with NFractionalD:
, NCaputoD coincides with NFractionalD:
Possible Issues (2)
NCaputoD will generate an error message if the precision of input is less than the WorkingPrecision:
NCaputoD takes only numeric points of evaluation:
Neat Examples (1)
Plot the Sin function and its half, first and ![]() -order derivatives:
-order derivatives:
Tech Notes
Related Guides
History
Text
Wolfram Research (2022), NCaputoD, Wolfram Language function, https://reference.wolfram.com/language/ref/NCaputoD.html.
CMS
Wolfram Language. 2022. "NCaputoD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NCaputoD.html.
APA
Wolfram Language. (2022). NCaputoD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NCaputoD.html
BibTeX
@misc{reference.wolfram_2025_ncaputod, author="Wolfram Research", title="{NCaputoD}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/NCaputoD.html}", note=[Accessed: 11-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ncaputod, organization={Wolfram Research}, title={NCaputoD}, year={2022}, url={https://reference.wolfram.com/language/ref/NCaputoD.html}, note=[Accessed: 11-January-2026]}