FunctionSign[f,{x1,x2,…}]
finds the real sign of the function f with variables x1,x2,… over the reals.
FunctionSign[f,{x1,x2,…},dom]
finds the real sign with variables restricted to the domain dom.
FunctionSign[{f,cons},{x1,x2,…},dom]
gives the sign when variables are restricted by the constraints cons.


FunctionSign
FunctionSign[f,{x1,x2,…}]
finds the real sign of the function f with variables x1,x2,… over the reals.
FunctionSign[f,{x1,x2,…},dom]
finds the real sign with variables restricted to the domain dom.
FunctionSign[{f,cons},{x1,x2,…},dom]
gives the sign when variables are restricted by the constraints cons.
Details and Options


- Function sign is also known as positive, non-negative, negative, non-positive, strictly positive and strictly negative.
- By default, the following definitions are used:
-

+1 non-negative, i.e. 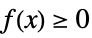 for all
for all 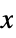

0 identically zero, i.e. 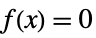 for all
for all 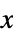
-1 non-positive, i.e. 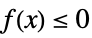 for all
for all 
Indeterminate neither non-negative nor non-positive - The zero function is both non-negative and non-positive.
- With the setting StrictInequalitiesTrue, the following definitions are used:
-
+1 positive, i.e. 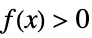 for all
for all 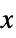
-1 negative, i.e. 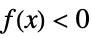 for all
for all 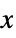
Indeterminate neither positive nor negative - Possible values for dom include: Reals, Integers, PositiveReals, PositiveIntegers, etc. The default is Reals.
- The function f should be a real-valued function for all xi in the domain dom that satisfy the constraints cons.
- cons can contain equations, inequalities or logical combinations of these.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions True whether to generate conditions on parameters PerformanceGoal $PerformanceGoal whether to prioritize speed or quality StrictInequalities False whether to require a strict sign - Possible settings for GenerateConditions include:
-
Automatic nongeneric conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal are "Speed" and "Quality".
Examples
open all close allBasic Examples (3)
Scope (7)
A function that is not real valued has an Indeterminate sign:
The function is real valued and non-negative for positive ![]() :
:
Univariate functions with constraints on the variable:
The strict sign of a function:
![]() is non-negative, but not strictly positive:
is non-negative, but not strictly positive:
Options (5)
Assumptions (1)
FunctionSign gives a conditional answer here:
GenerateConditions (2)
By default, FunctionSign may generate conditions on symbolic parameters:
With GenerateConditionsNone, FunctionSign fails instead of giving a conditional result:
This returns a conditionally valid result without stating the condition:
By default, all conditions are reported:
With GenerateConditions->Automatic, conditions that are generically true are not reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
StrictInequalities (1)
By default, FunctionSign computes the non-strict sign:
With StrictInequalitiesTrue, FunctionSign computes the strict sign:
![]() is non-negative, but not strictly positive.
is non-negative, but not strictly positive. ![]() is strictly positive:
is strictly positive:
Applications (14)
Basic Applications (3)
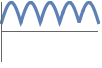
The graph of ![]() lies in the upper half-plane:
lies in the upper half-plane:
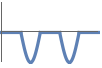
The graph of ![]() lies in the lower half-plane:
lies in the lower half-plane:
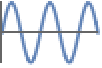
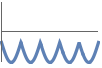
The graph of ![]() is not contained in either the upper or the lower half-plane:
is not contained in either the upper or the lower half-plane:
Show that ![]() restricted to
restricted to ![]() is non-negative:
is non-negative:
The sum of functions with sign ![]() has sign
has sign ![]() :
:
The sign of the product of functions is the product of signs:
Calculus (6)
The derivative of a non-decreasing function is non-negative:
If ![]() is non-negative, then
is non-negative, then ![]() , for
, for ![]() , is non-negative:
, is non-negative:
A sequence is non-decreasing iff its differences are non-negative:
Sums of non-negative sequences are non-decreasing:
Check the convergence of a non-negative series using d'Alembert's criterion:
Test whether the limit of ![]() is less than
is less than ![]() :
:
Prove that the integral ![]() is divergent:
is divergent:
Show that the integral of ![]() is divergent:
is divergent:
Probability & Statistics (3)
Geometry (2)
RegionDistance is always non-negative:
Integral of a non-negative function over a region is non-negative:
Properties & Relations (2)
The sum and product of non-negative functions are non-negative:
A continuous anti-derivative of a non-negative function is non-decreasing:
Use Integrate to compute an anti-derivative:
Use FunctionContinuous to check that the anti-derivative is continuous:
Use FunctionMonotonicity to verify that the anti-derivative is non-decreasing:
Related Guides
History
Text
Wolfram Research (2020), FunctionSign, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSign.html.
CMS
Wolfram Language. 2020. "FunctionSign." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSign.html.
APA
Wolfram Language. (2020). FunctionSign. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSign.html
BibTeX
@misc{reference.wolfram_2025_functionsign, author="Wolfram Research", title="{FunctionSign}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSign.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionsign, organization={Wolfram Research}, title={FunctionSign}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSign.html}, note=[Accessed: 17-February-2026]}