FunctionSign

FunctionSign[f,{x1,x2,…}]

変数が x1,x2,…の関数 f の実数上での実際の符号を求める．

FunctionSign[f,{x1,x2,…},dom]

領域 dom に制限される変数による実際の記号を求める．

FunctionSign[{f,cons},{x1,x2,…},dom]

変数が制約条件 cons によって制限されているときの符号を与える．

詳細とオプション

  • 関数の符号は，正，非負，負，非正，狭義の正，狭義の負としても知られている．
  • デフォルトで，次の定義が使われる．
  • +1非負，つまり，すべての 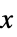について
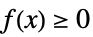
    0恒等的にゼロ，つまり，すべての 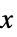について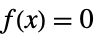
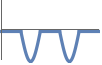
    -1非正，つまり，すべての 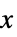について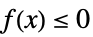
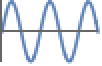
    Indeterminate非負でも非正でもない
  • ゼロ関数は非負でも非正でもない．
  • StrictInequalitiesTrueの設定のときは，次の定義が使える．
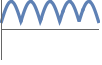
  • +1正，つまり，すべての 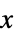について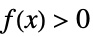
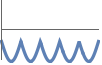
    -1負，つまり，すべての 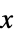について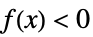
    Indeterminate正でも負でもない
  • dom の可能な値には，Reals，Integers，PositiveReals，PositiveIntegers等がある．デフォルトはRealsである．
  • 関数 f は，制約条件 cons を満足する領域 dom で，すべての xiについて実数値関数でなければならない．
  • cons には，等式，不等式，これらの論理結合を含めることができる．
  • 次は，使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Trueパラメータについての条件を生成するかどうか
    PerformanceGoal $PerformanceGoal速度または質を優先させるかどうか
    StrictInequalities False狭義の符号を必要とするかどうか
  • GenerateConditionsの可能な設定には以下がある．
  • Automatic一般的ではない条件のみ
    Trueすべての条件
    False条件なし
    None条件が必要なときは未評価で返す
  • PerformanceGoalの可能な設定は"Speed"と"Quality"である．

例題

すべて開くすべて閉じる

例  (3)

関数の符号を求める：

変数が条件によって制限されている関数の符号を求める：

関数の符号を整数上で求める：

スコープ  (7)

一変量関数：

実数値ではない関数の符号はIndeterminateである：

この関数は，正の については実数値で非負である：

変数に制約がある一変量関数：

関数の狭義の符号：

は非負だが狭義の正ではない：

多変量関数：

変数に制約がある多変量関数：

記号パラメータを持つ関数：

オプション  (5)

Assumptions  (1)

FunctionSignは以下では条件付きの答を与えている：

仮定を加えると関数は逆の符号になる：

GenerateConditions  (2)

デフォルトで，FunctionSignは記号パラメータに対して条件を生成することがある：

GenerateConditionsNoneとすると，FunctionSignは条件付きの結果を与えずに失敗する：

以下は条件付きで有効な結果を条件は述べずに与える：

デフォルトで，すべての条件が報告される：

GenerateConditions->Automaticとすると，一般に真である条件は報告されない：

PerformanceGoal  (1)

PerformanceGoalを使って潜在的に高価な計算を避ける：

デフォルト設定は使用可能なすべてのテクニックを使って結果を出そうとする：

StrictInequalities  (1)

デフォルトで，FunctionSignは広義の符号を計算する：

StrictInequalitiesTrueとすると，FunctionSignは狭義の符号を計算する：

は非負であるが，狭義の正ではない．は狭義の正である：

アプリケーション  (14)

基本的なアプリケーション  (3)

の符号をチェックする：

のグラフは上半平面にある：

の符号をチェックする：

のグラフは下半平面にある：

の符号をチェックする：

のグラフは上半平面あるいは下半平面だけにあるわけではない：

に限定されるは非負である：

符号 の関数の和の符号は である：

関数の積の符号は符号の積である：

微積分  (6)

非減少関数の導関数は非負である：

が非負なら， のとき は非負である：

数列は，その差が非負であるときかつそのときに限り，非減少である：

非負の数列の和は非減少である：

非負の数列の収束をダランベール(d'Alembert)の判定法を使ってチェックする：

の非負性をチェックする：

の極限がより小さいかどうか調べる：

積分 が発散することを証明する：

であることを示す：

が非負であることを示す：

の積分が発散することを示す：

確率と統計  (3)

PDFは常に非負である：

CDFは常に非負である：

SurvivalFunctionは常に非負である：

幾何  (2)

RegionDistanceは常に非負である：

非負の関数の定義域上での積分は非負である：

特性と関係  (2)

非負の関数の総和と積は非負である：

非負の関数の連続非導関数は非減少である：

Integrateを使って不定積分を求める：

FunctionContinuousを使って不定積分が連続であることを確かめる：

FunctionMonotonicityを使って不定積分が非減少であることを確かめる：

関数と不定積分をプロットする：

考えられる問題  (1)

関数が固定の符号を持つためには，関数をあらゆるところで定義しなければならない：

Wolfram Research (2020), FunctionSign, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionSign.html.

テキスト

Wolfram Research (2020), FunctionSign, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionSign.html.

CMS

Wolfram Language. 2020. "FunctionSign." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSign.html.

APA

Wolfram Language. (2020). FunctionSign. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSign.html

BibTeX

@misc{reference.wolfram_2024_functionsign, author="Wolfram Research", title="{FunctionSign}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSign.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionsign, organization={Wolfram Research}, title={FunctionSign}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSign.html}, note=[Accessed: 03-December-2024 ]}