FunctionSign
FunctionSign[f,{x1,x2,…}]
变量 x1,x2,… 为实数,求函数的 f 正负性.
FunctionSign[f,{x1,x2,…},dom]
变量被限制在域 dom 内,求函数的正负性.
FunctionSign[{f,cons},{x1,x2,…},dom]
当变量受约束条件 cons 限制时,求函数的正负性.
更多信息和选项
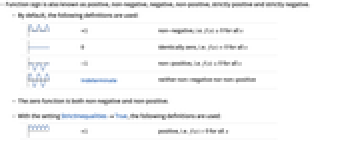

- 函数的正负性亦称为正、非负、负、非正、严格正和严格负.
- 默认情况下,可使用以下定义:
-

+1 非负,即对于所有的 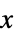 ,
,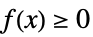

0 全部为零,即对于所有的 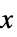 ,
,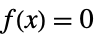
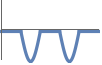
-1 非正,即对于所有的 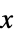 ,
,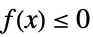
Indeterminate 既不是非负,也不是非正 - 零函数既是非负的,也是非正的.
- 如果设置 StrictInequalitiesTrue,可使用以下定义:
-
+1 正的,即对于所有的 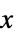 ,
,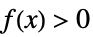
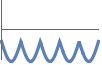
-1 负的,即对于所有的 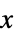 ,
,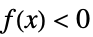
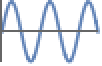
Indeterminate 既非负,亦非正 - dom 的可能的值包括:Reals、Integers、PositiveReals、PositiveIntegers 等. 默认值为 Reals.
- 对于 dom 中满足约束条件 cons 的所有 xi,f 应为实值函数.
- cons 可以包含等式、不等式或它们的逻辑组合.
- 可给出以下选项:
-
Assumptions $Assumptions 对参数的设定 GenerateConditions True 是否生成关于参数的条件 PerformanceGoal $PerformanceGoal 优先考虑速度还是质量 StrictInequalities False 是否要求严格正负性 - GenerateConditions 的可能的设置包括:
-
Automatic 只给出非通用条件 True 所有条件 False 不给出条件 None 如果需要条件则不经计算直接返回 - PerformanceGoal 的可能设置为 "Speed" 和 "Quality".
范例
打开所有单元关闭所有单元范围 (7)
非实值函数的正负性为 Indeterminate:
选项 (5)
Assumptions (1)
FunctionSign 给出有条件的答案:
GenerateConditions (2)
默认情况下,FunctionMonotonicity 可能会对符号参数生成条件:
如果设置 GenerateConditionsNone,FunctionSign 会失败,而不是给出有条件的结果:
如果设置 GenerateConditions->Automatic,不报告通常为真的条件:
PerformanceGoal (1)
用 PerformanceGoal 避免潜在费时的计算:
StrictInequalities (1)
应用 (14)
基本应用 (3)
微积分 (6)
概率与统计 (3)
几何 (2)
属性和关系 (2)
文本
Wolfram Research (2020),FunctionSign,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FunctionSign.html.
CMS
Wolfram 语言. 2020. "FunctionSign." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSign.html.
APA
Wolfram 语言. (2020). FunctionSign. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FunctionSign.html 年