GainPhaseMargins[lsys]
gives the gain and phase margins of the linear time-invariant system lsys.


GainPhaseMargins
GainPhaseMargins[lsys]
gives the gain and phase margins of the linear time-invariant system lsys.
Details and Options

- The system lsys can be a TransferFunctionModel or a StateSpaceModel.
- GainPhaseMargins returns {{{ωp1,g1},{ωp2,g2},…},{{ωg1,p1},{ωg2,p2},…}}, where the ωpi are the phase crossover frequencies, the gi are the gain margins, the ωgi are the gain crossover frequencies, and the pi are the phase margins.
- The gain margins gi are absolute values and the phase margins pi are in radians.
- The gain margins are the reciprocals of the magnitude of lsys at the phase crossover frequencies.
- At the phase crossover frequencies, lsys has phase
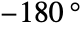 .
. - The phase margins are phase lags needed to make the phase
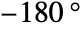 at the gain crossover frequencies.
at the gain crossover frequencies. - At the gain crossover frequencies, the gain of lsys is unity.
- The following options can be given:
-
FeedbackType "Negative" the feedback type Method Automatic method to use SamplingPeriod None the sampling period - Explicit settings for the Method option include "Solve" and "NSolve". In each case the methods of Solve or NSolve can be specified as suboptions. The default setting of Automatic switches between these methods, depending on whether lsys is exact or inexact.
- GainPhaseMargins has the attribute Listable.
Examples
open all close allScope (3)
Generalizations & Extensions (1)
GainPhaseMargins[TransferFunctionModel[g,var]] equals GainPhaseMargins[g]:
Options (2)
Properties & Relations (2)
The gain and phase margins can be visualized on all the frequency response plots:
If the crossover frequencies are in radians/second, they can be converted to hertz as follows:
The setting StabilityMargins->True computes and draws the gain and phase margins:
Related Guides
History
Text
Wolfram Research (2010), GainPhaseMargins, Wolfram Language function, https://reference.wolfram.com/language/ref/GainPhaseMargins.html.
CMS
Wolfram Language. 2010. "GainPhaseMargins." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GainPhaseMargins.html.
APA
Wolfram Language. (2010). GainPhaseMargins. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GainPhaseMargins.html
BibTeX
@misc{reference.wolfram_2025_gainphasemargins, author="Wolfram Research", title="{GainPhaseMargins}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/GainPhaseMargins.html}", note=[Accessed: 09-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_gainphasemargins, organization={Wolfram Research}, title={GainPhaseMargins}, year={2010}, url={https://reference.wolfram.com/language/ref/GainPhaseMargins.html}, note=[Accessed: 09-February-2026]}