GaussianMatrix

GaussianMatrix[r]

半径 r のガウス(Gauss)カーネルに相当する行列を与える．

GaussianMatrix[{r,σ}]

半径 r，標準偏差 σ のガウスカーネルに相当する行列を与える．

GaussianMatrix[r,{n1,n2}]

ガウス行列の行に関しては n1次の導関数から，列に関しては n2次の導関数から形成される行列を与える．

GaussianMatrix[r,{{n11,n12},{n21,n22},…}]

ni1導関数と ni2導関数の和から形成される行列を返す．

GaussianMatrix[{{r1,r2,…},σ},…]

第 i 指標方向で半径 riのガウスカーネルに相当する配列を与える．

詳細とオプション

  • GaussianMatrix[r]は中心からの指標位置 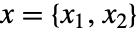で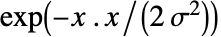を近似する値を与える．ただし，σ=r/2である．
  • デフォルトで，GaussianMatrix[r]の要素の和は1である．
  • GaussianMatrix[…,{n1,n2}]は，デフォルトで，離散導関数を有限差分として構築する．
  • GaussianMatrix[r,{{2,0},{0,2}}]はLOG(Laplacian-of-Gaussian)変換から形成される行列を返す．
  • GaussianMatrix[{Automatic,σ,f},…]は，各方向にガウス行列の離散積分に対して少なくとも f の割合を含むのに十分な大きさの行列を構築する．
  • r，σ，f の任意のものが，異なる方向に異なる値を指定するリストになることができる．
  • 整数 r について，GaussianMatrix[r,…]は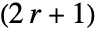×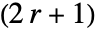行列を返す．
  • 非整数 r について，r の値は事実上整数に丸められる．
  • 指定可能なオプション
  • Method "Bessel"行列要素の決め方
    Standardized True切断を考慮するために行列を再スケールしたりシフトしたりするかどうか
    WorkingPrecision Automatic行列要素の計算に使う精度
  • Methodオプションの使用可能な設定値には"Bessel"と"Gaussian"がある．
  • デフォルトのオプション設定のMethod->"Bessel"では，GaussianMatrix[r]はproduct_(i=1)^2exp(-sigma^2) TemplateBox[{{x, _, i}, {sigma, ^, 2}}, BesselI]に比例する要素を持ち，最適な離散たたみ込み特性を持つカーネルを返す．
  • Method->"Bessel"では，ガウスの導関数は有限差分演算子で得ることができる．GaussianMatrix[{r,}]は有限差分方程式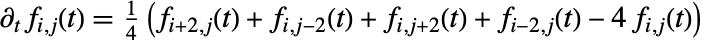を満足する．
  • Method->"Gaussian"では，GaussianMatrix[r]は生の連続的な関数形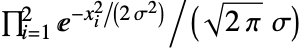に比例する要素を持つ．
  • Method->"Gaussian"では，ガウスの導関数は関数形式の偏導関数に比例する．GaussianMatrix[{r,}]は微分方程式 をほぼ満足する．
  • Standardized->Trueとすると，比例因子によってGaussianMatrix[r]の要素の和が1になることが確かになる．しかし，少なくとも1つの非零要素 niを含むGaussianMatrix[r,{n1,n2,…}]の要素の和は0になり，各方向に原点から niのベキ乗までの距離の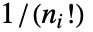倍で重みを付けた要素の和は1になる．
  • Standardized->Falseとすると比例因子は使われない．

予備知識

  • GaussianMatrixは，ガウス分布に従う行列を返すコンストラクタ関数である．このような行列は，平滑化あるいは画像の導関数を取るためのたたみ込みにおけるカーネルとして使われることが多い．
  • 関数ImageConvolveを使ってガウス行列カーネルを使った画像のたたみ込みを行うことができる．平滑化カーネル行列あるいは導関数カーネル行列を作成するその他の関数に，ShenCastanMatrixおよびSavitzkyGolayMatrixがある．非平滑化カーネルもまた画像の平滑化に使えることに注意のこと．この目的でよく使われるバイナリカーネルにはDiskMatrix，DiamondMatrixおよびその他の同様の関数がある．

例題

すべて開くすべて閉じる

例  (3)

ガウス行列を計算しプロットする：

ガウスベクトルを計算しプロットする：

水平次元におけるガウス行列の1次導関数：

スコープ  (6)

半径20のガウス行列：

行列の3Dプロット：

標準偏差が変化するガウス行列：

ガウス行列の垂直方向の一次導関数：

ガウス行列の水平方向の一次導関数：

行列の3D可視化：

3Dガウス配列を作成し，可視化する：

3D導関数カーネル：

1次元に沿った3D導関数カーネル：

一般化と拡張  (4)

厳密な記号ガウス行列を生成する：

標準偏差の2倍の半径を使う：

少なくともガウス行列の所望の部分を埋めるに足る半径を使う：

これより小さい半径を使うと所望の部分は与えられなかったであろう：

指定の半径がガウス行列の所望の部分を与えるような標準偏差を使う：

オプション  (10)

Method  (4)

Method->"Bessel"とすると，導関数は有限差分を使って計算される：

Method->"Gaussian"では，連続微分が使われる：

離散たたみ込みに適したガウス行列：

連続体からサンプルとして取られたガウス行列：

Standardized  (5)

正規化されたガウスベクトル：

正規化されたガウス行列：

正規化されていないガウスベクトル：

正規化されていない行列の合計は，その大きさと標準偏差の比が大きくなるにつれて1に近付く：

シフトされたガウスの導関数：

シフトされたガウスの導関数も再スケールされる：

標準化されていないガウスの導関数：

シフトと再スケールは，すべてのメソッドについて離散正規化を使って行われる：

WorkingPrecision  (1)

機械精度のガウスベクトル：

厳密な記号ガウスベクトル：

高精度のガウスベクトル：

アプリケーション  (3)

信号の平滑化：

画像のガウスぼかしを適用する：

画像の鉛直微分を計算する：

考えられる問題  (1)

少なくとも半径か標準偏差の1つが各方向に指定されなければならない：

Wolfram Research (2008), GaussianMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaussianMatrix.html （2015年に更新）.

テキスト

Wolfram Research (2008), GaussianMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaussianMatrix.html （2015年に更新）.

CMS

Wolfram Language. 2008. "GaussianMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GaussianMatrix.html.

APA

Wolfram Language. (2008). GaussianMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianMatrix.html

BibTeX

@misc{reference.wolfram_2024_gaussianmatrix, author="Wolfram Research", title="{GaussianMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gaussianmatrix, organization={Wolfram Research}, title={GaussianMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaussianMatrix.html}, note=[Accessed: 21-November-2024 ]}