GaussianMatrix

GaussianMatrix[r]

给出一个矩阵，该矩阵对应于半径为 r 的高斯核.

GaussianMatrix[{r,σ}]

给出一个矩阵，该矩阵对应于半径为 r、标准偏差为 σ 的高斯核.

GaussianMatrix[r,{n1,n2}]

给出一个矩阵，该矩阵由高斯函数沿行的 n1 阶导数和沿列的 n2 阶导数形成.

GaussianMatrix[r,{{n11,n12},{n21,n22},…}]

给出一个矩阵，由 ni1 和 ni2 阶导数的和形成.

GaussianMatrix[{{r1,r2,…},σ},…]

给出一个数组，该数组对应于第 i 个索引方向上半径为 ri 的高斯核.

更多信息和选项

  • GaussianMatrix[r] 给出在离中心的索引位置 上 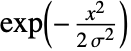的近似值，其中 σ=r/2.
  • 默认情况下，GaussianMatrix[r] 的元素的和是 1.
  • GaussianMatrix[…,{n1,n2}] 默认按有限差分构建离散导数.
  • GaussianMatrix[r,{{2,0},{0,2}}] 给出由高斯的拉普拉斯形成的矩阵.
  • GaussianMatrix[{Automatic,σ,f},…] 构建一个矩阵，大到恰好在每个方向上至少包含一个高斯离散积分的分数 f 倍.
  • 允许任何的 r、σ 和 f 采用列表形式，指定不同方向上的不同值.
  • 对于整数 r，GaussianMatrix[r,…] 产生一个 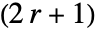× 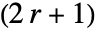的矩阵.
  • 对于非整数 r，r 的值实际舍入成整数.
  • 可以指定下列选项：
  • Method "Bessel"如何确定矩阵元素
    Standardized True在截断时是否考虑对矩阵进行缩放和平移
    WorkingPrecision Automatic计算矩阵元素所用的精度
  • Method 选项的可能设置为 "Bessel" 和 "Gaussian".
  • 在默认选项设置 Method->"Bessel" 下，GaussianMatrix[r] 的元素正比于 product_(i=1)^2exp(-sigma^2) TemplateBox[{{x, _, i}, {sigma, ^, 2}}, BesselI]，产生一个具有最优离散卷积性质的核.
  • 对于 Method->"Bessel", 高斯的导数由有限差分算子得到. GaussianMatrix[{r,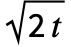}] 满足有限差分方程 .
  • 在 Method->"Gaussian" 下，GaussianMatrix[r] 的元素正比于原始连续函数形式 .
  • 对于 Method->"Gaussian"，高斯的导数与函数形式的偏导数成正比. GaussianMatrix[{r,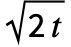}] 近似满足微分方程 .
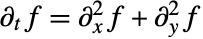  • 设置 Standardized->True 时，比例因子确保 GaussianMatrix[r] 的元素和为 1. 但是，GaussianMatrix[r,{n1,n2,…}] 的元素在至少有一个非零 ni 时的和为 0，而在每个方向上以从原点距离的 ni 次幂的 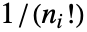倍的值加权时，元素的和为 1.
  • 设置 Standardized->False 时，不使用比例因子.

背景

  • GaussianMatrix 是高斯线型矩阵的构造函数. 这样的矩阵通常被用作平滑图像或计算衍生图像的图像卷积的核.
  • 函数 ImageConvolve 可利用高斯矩阵核对图像做卷积. 其它产生平滑或衍生核矩阵的函数包括 ShenCastanMatrix 和 SavitzkyGolayMatrix. 请注意非平滑核也可被用于平滑图像. 通常可作此用途的二元内核包括 DiskMatrix、DiamondMatrix，以及其它类似函数.

范例

打开所有单元关闭所有单元

基本范例  (3)

计算并绘制一个高斯矩阵：

计算并且绘制高斯向量：

在水平方向上高斯矩阵的一次导数：

范围  (6)

给出半径为 20 情况下的高斯矩阵：

矩阵的三维图：

不同标准偏差的高斯矩阵：

高斯矩阵在垂直维度上的一阶导数：

高斯矩阵在水平维度上的一阶导数：

矩阵的三维图：

创建并可视化三维高斯阵列：

三维导数核：

沿着第一个维度的三维导数核：

推广和延伸  (4)

产生一个精确符号式的高斯矩阵：

使用标准差的两倍作为半径：

使用足够填充至少高斯矩阵的期望分数的值作为半径：

使用较小的半径可能无法提供期望的分数：

使用标准差，满足指定半径可提供高斯矩阵的期望分数：

选项  (10)

Method  (4)

在 Method->"Bessel" 选项下，使用有限差分计算导数：

在 Method->"Gaussian" 选项下，则使用连续导数：

适用于离散卷积的高斯矩阵：

从连续谱上采样得到的高斯矩阵：

Standardized  (5)

归一化高斯向量：

归一化高斯矩阵：

非归一化的高斯向量：

当矩阵的大小与标准偏差的比增加时，未归一化的矩阵的总和接近1：

平移的高斯导数：

平移的高斯导数也是被缩放的：

未标准化的高斯导数：

对所有方法使用离散归一化来执行平移和缩放：

WorkingPrecision  (1)

机器精度的高斯向量：

精确的符号高斯向量：

高精度高斯向量：

应用  (3)

信号的平滑：

对图像应用高斯模糊处理：

计算图像的垂直导数：

可能存在的问题  (1)

在每个方向上必须指定至少一个半径或者标准差：

Wolfram Research (2008)，GaussianMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GaussianMatrix.html （更新于 2015 年）.

文本

Wolfram Research (2008)，GaussianMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GaussianMatrix.html （更新于 2015 年）.

CMS

Wolfram 语言. 2008. "GaussianMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GaussianMatrix.html.

APA

Wolfram 语言. (2008). GaussianMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GaussianMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_gaussianmatrix, author="Wolfram Research", title="{GaussianMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianMatrix.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gaussianmatrix, organization={Wolfram Research}, title={GaussianMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaussianMatrix.html}, note=[Accessed: 21-November-2024 ]}