GeoOrientationData[date,prop]
gives the value of the property prop about the orientation of the Earth on the given date.
GeoOrientationData[date,prop,"variant"]
gives the specified variant of the property prop on the given date.


GeoOrientationData
GeoOrientationData[date,prop]
gives the value of the property prop about the orientation of the Earth on the given date.
GeoOrientationData[date,prop,"variant"]
gives the specified variant of the property prop on the given date.
Details




- GeoOrientationData gives information about the orientation of the Earth with respect to the celestial reference frame.
- GeoOrientationData is typically used in applications such as pointing a telescope, monitoring the rotation and wobble of the Earth, or investigating how Earth's rotation has slowed down in the past.
- The gravitational pull of other celestial bodies, the internal motion of mass in the Earth, ocean tides and other physical phenomena modify the average rotation of the Earth and the direction of its rotation axis in unpredictable ways. The consequences of many of those effects are tracked in GeoOrientationData.
- In GeoOrientationData[date,…], date specifications are DateObject or DateInterval expressions representing dates or intervals. The TimeSystem option of DateObject allows specifying time systems such as "UT1" or "TT", with default "UTC".
- Temporal properties describing the inhomogeneous duration of the day include:
-
"DayDuration" duration in seconds of the day of the given date "DayDurationExcess" excess of the duration of the day over 86400 seconds "LeapSecondCount" number of leap seconds inserted until the given date "LeapSeconds" list of leap seconds added during a given period "TAIMinusUTC" difference between TAI and UTC times "TTMinusUT1" difference between TT and UT1 times "UT1MinusUTC" difference between UT1 and UTC times - Properties describing Earth's precession motion include:
-
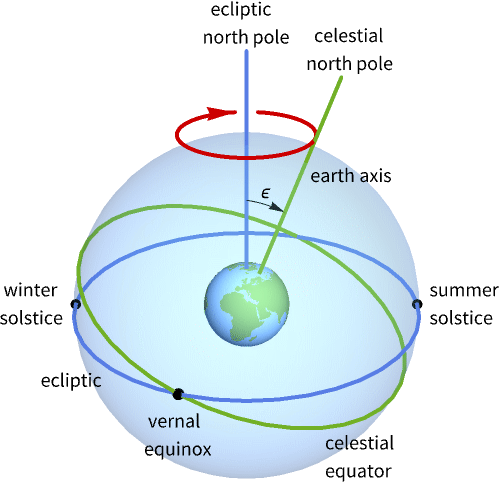
"BiasMatrix" rotation matrix from the ICRS frame to the mean equatorial frame of J2000 "PrecessionMatrix" rotation matrix from the mean equatorial frame of J2000 to the mean equatorial frame of date "MeanObliquity" angle between the mean equatorial and ecliptic planes "TrueObliquity" angle between the true equatorial and ecliptic planes "EquationOfEquinoxes" difference in right ascension between the true and mean equinoxes "EquationOfOrigins" difference in right ascension betwen the true equinox and the CIO point - Properties describing Earth's nutation motion include:
-
"LongitudeNutation" nutation 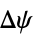 in the ecliptic longitude of Earth's rotation axis
in the ecliptic longitude of Earth's rotation axis"ObliquityNutation" nutation 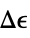 in the ecliptic latitude of Earth's rotation axis
in the ecliptic latitude of Earth's rotation axis"NutationAngles" 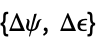 nutation angles of Earth's rotation axis
nutation angles of Earth's rotation axis"NutationMatrix" rotation matrix from the mean equatorial frame of date to the true equatorial frame of date - Properties describing Earth's rotation include:
-
"EarthRotationAngle" Earth's rotation angle measured from the CIO point "GreenwichMeanSiderealTime" Earth's rotation angle measured from the mean equinox "GreenwichApparentSiderealTime" Earth's rotation angle measured from the true equinox - Properties describing the orientation of the Earth with respect to the terrestrial reference frame include:
-
"PolarMotion" 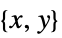 components of the rotation axis in the ITRF frame
components of the rotation axis in the ITRF frame"PolarMotionX" 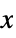 component of rotation axis, positive toward Greenwich
component of rotation axis, positive toward Greenwich"PolarMotionY" 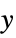 component of rotation axis, positive toward 90° west
component of rotation axis, positive toward 90° west"PolarMotionGeoPosition" geodetic location of the instantaneous rotation axis - In GeoOrientationData[date,prop,"variant"] possible variants include:
-
"Value" value of the property, a number, quantity or geo position "Uncertainty" uncertainty of the measured value, if available "Around" Around[value,uncertainty] object - For dates after 1960 until April 2023, measured data was obtained from the International Earth Rotation and Reference Systems Service (IERS), as well as predicted data from May 2023 to April 2024. Data before 1960 was obtained from the analysis of older astronomical sources, in particular, ancient observation of eclipses. Future data is extrapolated.
Examples
open all close allBasic Examples (3)
Get the difference between TAI and UT1 times at the beginning of January 1, 2000:
This number of leap seconds had been inserted by then to approximate that result:
Find the observed duration of July 19, 2020:
The excess over 86400 seconds is negative, so this day was shorter than the standard civil day:
Report the result with its uncertainty:
Find the geodetic location of the instantaneous rotational axis of the Earth for a given date:
Scope (7)
Specify dates as DateObject expressions:
Get property values for a list of dates:
Get a time series of property values for a DateInterval input:
Obtain the list of 27 leap seconds introduced since 1972:
There were no leap seconds added in the year 2020:
Mean obliquity angle ![]() between the mean equatorial and the ecliptic planes:
between the mean equatorial and the ecliptic planes:
Display the evolution of the mean obliquity angle for Julian years ![]() to
to ![]() :
:
Compute the difference in right ascension between the mean and true equinoxes:
It can also be computed with AstroPosition:
Plot the evolution of the nutation angles over a period of 18 years, almost a complete 18.6-year cycle:
Applications (4)
Find the excess in day durations for all days since January 1, 1962:
It has changed a few milliseconds in the last few decades:
Recently, the day has been getting shorter:
Show the behavior in the last few years:
Show the behavior in the last few months:
Find the difference between TAI and UT1 for the first day of each month since 1960:
Also get the difference between TAI and UTC, which was piecewise linear from 1960 to 1973 and is now piecewise constant:
UTC follows UT1 in such a way that their difference is never larger than 0.9 seconds:
Locate the instantaneous rotation axis with respect to the geodetic North Pole between 2010 and 2015:
The result is given as a list of pairs of the ![]() and
and ![]() components of the rotation axis, usually given as small angles with respect to the North Pole:
components of the rotation axis, usually given as small angles with respect to the North Pole:
The standard convention makes the ![]() axis point toward Greenwich on the left and the
axis point toward Greenwich on the left and the ![]() axis toward 90 degrees west on the top:
axis toward 90 degrees west on the top:
Convert to a representation in meters:
Average the polar motion of the instantaneous rotation axis around the geodetic North Pole:
Properties & Relations (8)
Plot the jumps of the 27 leap seconds introduced since 1972:
Each jump corresponds to a second:
The long-term behavior of TT-UT1 is parabolic:
Atomic time TAI was synchronized with UT1 at the beginning of 1958:
Compute the mean sidereal time at zero longitude on a given date:
This can also be computed with SiderealTime at any location with zero longitude:
Compute the apparent sidereal time at zero longitude on a given date:
This can also be computed with SiderealTime at any location with zero longitude:
Compute the angle between the North Celestial Pole and the North Ecliptic Pole:
It can also be computed with AstroAngularSeparation:
Or with AstroPosition, using the true ecliptic frame:
Or with AstroPosition, using the true equatorial, true equinox (TETE) frame:
Compute the difference in right ascension between the mean and true equinoxes:
It can also be computed with AstroPosition:
Find the right ascension difference between the true equinox and the celestial intermediate origin (CIO):
It can be computed with AstroAngularSeparation:
Or with AstroPosition, using the true equatorial, true equinox (TETE) frame:
Or with AstroPosition, using the celestial intermediate reference system (CIRS) frame:
Related Guides
Text
Wolfram Research (2021), GeoOrientationData, Wolfram Language function, https://reference.wolfram.com/language/ref/GeoOrientationData.html (updated 2023).
CMS
Wolfram Language. 2021. "GeoOrientationData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/GeoOrientationData.html.
APA
Wolfram Language. (2021). GeoOrientationData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeoOrientationData.html
BibTeX
@misc{reference.wolfram_2025_geoorientationdata, author="Wolfram Research", title="{GeoOrientationData}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/GeoOrientationData.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_geoorientationdata, organization={Wolfram Research}, title={GeoOrientationData}, year={2023}, url={https://reference.wolfram.com/language/ref/GeoOrientationData.html}, note=[Accessed: 11-March-2026]}