AstroPosition[{az,alt}]
defines a location on the celestial sphere with azimuth az and altitude alt in the current horizontal frame at your geo position.
AstroPosition[{az,alt,r}]
defines a location in celestial space with horizon coordinates az,alt and at distance r from your geo position.
AstroPosition[coords,frame]
uses the given frame, such as "Equatorial", "Horizon", "Galactic", etc. to define the orientation and meaning of the spherical coordinates coords.
AstroPosition[coords,frame,csys]
represents a location in celestial space given by a list of numeric coords referenced to the given frame and using the coordinate system csys, such as "Cartesian", "Cylindrical", etc.
AstroPosition[{coords1,coords2,…},frame,csys]
represents an array of celestial locations.
AstroPosition[entity,frame,csys]
returns the position of entity with respect to the given frame and coordinate system.




AstroPosition
AstroPosition[{az,alt}]
defines a location on the celestial sphere with azimuth az and altitude alt in the current horizontal frame at your geo position.
AstroPosition[{az,alt,r}]
defines a location in celestial space with horizon coordinates az,alt and at distance r from your geo position.
AstroPosition[coords,frame]
uses the given frame, such as "Equatorial", "Horizon", "Galactic", etc. to define the orientation and meaning of the spherical coordinates coords.
AstroPosition[coords,frame,csys]
represents a location in celestial space given by a list of numeric coords referenced to the given frame and using the coordinate system csys, such as "Cartesian", "Cylindrical", etc.
AstroPosition[{coords1,coords2,…},frame,csys]
represents an array of celestial locations.
AstroPosition[entity,frame,csys]
returns the position of entity with respect to the given frame and coordinate system.
Details



- AstroPosition represents observed astronomical positions on the celestial sphere or in spacetime. It plays the role in astronomy that GeoPosition plays in geography.
- Celestial coordinates are always referred to a frame, an oriented triple of orthogonal axes centered at a definite location and using a particular time system.
- AstroPosition[coords] is equivalent to AstroPosition[coords,"Horizon","NorthAzAlt"].
- Possible inertial frames, not rotating with respect to distant stars and centered at the solar system barycenter, include:
-
"ICRS" or "BCRS" international celestial reference system "J2000" mean equatorial, mean equinox of date J2000 "B1950" mean equatorial, mean equinox of date B1950 "Galactic" inertial frame oriented along the plane of the Milky Way - Non-inertial frames centered at Earth's center but not rotating with the Earth include:
-
"GCRS" geocentric celestial reference system "MEME" frame oriented along Earth's mean equator and using the mean equinox as 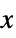 axis
axis"TETE" or "Equatorial" frame oriented along Earth's true equator and using the true equinox as 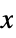 axis
axis"CIRS" celestial intermediate reference system "MeanEcliptic" frame oriented along the ecliptic and using the mean equinox as 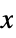 axis
axis"TrueEcliptic" or "Ecliptic" frame oriented along the ecliptic and using the true equinox as 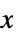 axis
axis - Non-inertial frames rotating with the Earth include:
-
"TIRS" terrestrial intermediate reference system, centered at Earth's center and sharing the same polar axis as "CIRS" "ITRS" international terrestrial reference system, centered at Earth's center and corotating with the ellipsoidal Earth "Horizon" frame oriented along the local horizontal plane at a given geo location and centered at that location - Possible parameters for a frame of the form {"frame", "param1"val1, "param2"val2,…} include:
-
"LightTime" whether to use geometric, retarded or advanced coordinates "LightDeflection" whether to correct for deflection of light by massive bodies "GravitationalTimeDelay" whether to correct for Shapiro time delay "Aberration" whether to correct for aberration, due to observer motion "PrecessionNutationModel" model of precession and nutation used "Date" or "ObservationDate" date of observation "Location" origin of the frame and location of observation "Epoch" or "FrameDefinitionEpoch" date defining the orientation of rotating frames "PolarMotion" coordinates {x',y'} of the ITRS 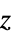 axis in the TIRS frame
axis in the TIRS frame"Refraction" values of pressure, temperature, relative humidity and wavelength for the computation of atmospheric refraction - {"frame","Date"date,"Location"loc,otherparams} can also be given as {"frame",date,loc,otherparams}.
- Given a frame, different coordinate systems csys can be used: "Spherical", "Cylindrical", "Cartesian" or projections of the spherical coordinates like "Mollweide", "Mercator" and others. All spherical projections in GeoProjectionData["Spherical"] are available.
- AstroPosition downloads ephemeris data files for solar system objects, storing them permanently in FileNameJoin[{$UserAddOnsDirectory,"ApplicationData","Astro"}].
Examples
open all close allBasic Examples (6)
Specify a location on the celestial sphere by providing its azimuth and altitude angles in degrees:
Specify a location in 3D space by providing its azimuth, altitude and distance from your geo location:
Specify a location using Cartesian coordinates in Earth's mean ecliptic reference frame:
Find the current position of the Large Magellanic Cloud with respect to your horizontal frame:
Rotate those coordinates to the equatorial frame, oriented along Earth's equatorial plane:
Draw a circle around that location:
Current position of Mars in the International Celestial Reference System, centered at the solar system barycenter, in Cartesian coordinates:
Extract the XYZ coordinate vector, in astronomical units:
Find the Earth-centered equatorial coordinates of Jupiter on a given date:
This was the distance between the centers of Jupiter and the Earth at that instant, in astronomical units:
Plot the evolution of such distance during the years 2015 to 2030, again in astronomical units:
Scope (34)
Coordinates (5)
Angular coordinates are stored using degrees, and distances are stored using astronomical units:
Specify an angular position on the celestial sphere, in the CIRS frame, assuming the current date:
Find the positions of a list of astro entities:
Provide coordinates using a QuantityArray object:
Frames (13)
AstroPosition uses by default the horizontal frame whose ![]() -
-![]() plane is tangent to the Earth at your geo location:
plane is tangent to the Earth at your geo location:
Use the galactic frame, whose space axes are oriented along the galactic plane and center and that is centered at the solar system barycenter:
Use the GCRS (Geocentric Coordinate Reference System) frame, whose space axes are oriented along the ICRS and that is centered at the geo center:
Use the MEME (mean equatorial, mean equinox) frame of a given epoch:
Use the J2000 frame, the mean equatorial, mean equinox frame of date J2000, very close to the ICRS frame:
Use the B1950 frame, the mean equatorial, mean equinox frame of date B1950:
Use the TETE (true equatorial, true equinox) frame of a given epoch:
Use the mean ecliptic frame of a given epoch:
Use the true ecliptic frame of a given epoch:
Use the CIRS (Celestial Intermediate Reference System) frame:
Use the TIRS (Terrestrial Intermediate Reference System) frame:
Use the ITRS (International Terrestrial Reference System) frame:
Observation Dates (4)
Specify the observation date as a DateObject expression:
Dates are taken in any time system and converted into the "TT" time system:
Date strings are assumed to be in the local time zone, the default smeared UTC time system, and are converted into "TT", in time zone 0:
Some especially important dates can be given as named strings:
Observation Locations (1)
Frame Epochs (1)
Astrometric Corrections (6)
Position of Mars at the current instant in the main BCRS coordinate system of the solar system:
Position of Mars when the light was emitted that arrived at Earth's center at that instant:
The difference is on the order of tens of arcseconds:
Position of Mars when receiving light emitted from Earth's center at that instant:
Eddington observed this star during a solar eclipse on May 29, 1919:
The Sun and Moon were essentially at the same position:
This was the observed position, including light deflection:
This would have been its position with no light deflection:
The difference is about one arcsecond:
The Shapiro effect introduces a small delay in light propagation for light rays that pass near massive bodies like the Sun, which also affects positions. Observe Venus on this date:
Differences are very small, in the order of microarcseconds:
Observed positions change due to the motion of the observer, for example, the orbital motion of the Earth around the Sun:
This is the current observed position of Polaris:
This would be its position with no correction for aberration:
Six months later, the aberration correction will have the opposite sign:
The instantaneous rotation axis of the Earth wobbles around the geographical polar axis of the Earth, introducing small corrections in the positions of objects with respect to the "ITRS" and "Horizon" frames:
The angular differences can be obtained from GeoOrientationData:
By default, the "ITRS" and "Horizon" frames use measured values of polar motion:
This would be the position of Sirius without taking into account polar motion:
Specify your own values of polar motion:
Compute the time of sunset on this date:
That is the time when the upper limb of the Sun touches the horizon on its way down, so the Sun's center already has negative altitude at that time:
By default, "Horizon" computations on Earth use a refraction model. Without it, this would have been the position of the Sun at that instant:
The difference is approximately 36 arcminutes for standard atmospheric conditions. Specify your own conditions of pressure, temperature and relative humidity, as well as the light wavelength:
Coordinate Systems (3)
Coordinates are given by default in spherical form, as longitude, latitude pairs:
Convert to Cartesian coordinates, still in the same equatorial frame:
Convert to cylindrical coordinates:
Express in a given cartographic projection:
Specify a location in the solar system in Cartesian coordinates of the ecliptic frame, in AUs:
Compute spherical horizontal coordinates for the Moon:
Compute SEU Cartesian coordinates:
Properties (1)
Extract properties from an AstroPosition object:
Extract coordinate properties:
Angles are given as numbers of angular degrees:
Distance from the frame origin is given in astronomical units:
Applications (4)
The Sun crosses the true equatorial plane on the equinox dates, making its declination zero:
Find the instant of the autumn equinox in year 2022:
Convert the date to the Gregorian calendar:
The Sun takes a tropical year to advance 360 degrees in ecliptic longitude:
The Sun takes a sidereal year to advance 360 degrees in right ascension with respect to an inertial frame:
The sidereal year is about 20 minutes longer, due to the precession of the equinoxes:
In late September 2022, Jupiter was in opposition to the Sun and therefore rising at sunset:
Take the current coordinates of Betelgeuse in the mean equatorial frame of epoch J2000:
Compute the change of coordinates of the star due to Earth's precession:
Compute the change of coordinates, now also adding the effect of nutation:
Properties & Relations (6)
The "J2000" frame is equivalent to the mean equatorial, mean equinox frame at the SSB with epoch "J2000":
When the location is the SSB, the astrometric corrections are deactivated automatically:
AstroPosition[![]() ,{"Horizon",date,loc}] is equivalent to SunPosition[date,loc,CelestialSystem"Horizon"]:
,{"Horizon",date,loc}] is equivalent to SunPosition[date,loc,CelestialSystem"Horizon"]:
AstroPosition[![]() ,{"Equatorial",date,loc}] is equivalent to SunPosition[date,loc,CelestialSystem"Equatorial"]:
,{"Equatorial",date,loc}] is equivalent to SunPosition[date,loc,CelestialSystem"Equatorial"]:
AstroPosition[![]() ,{"Horizon",date,loc}] is equivalent to MoonPosition[date,loc,CelestialSystem"Horizon"]:
,{"Horizon",date,loc}] is equivalent to MoonPosition[date,loc,CelestialSystem"Horizon"]:
AstroPosition[moon,{"Horizon",date,loc}] is equivalent to MoonPosition[date,loc,CelestialSystem"Horizon"]:
GeoPosition[loc] is equivalent to AstroPosition[loc,"ITRS"] for a spherical model of Earth:
The latitude difference is due to using an ellipsoidal model in GeoPosition and a spherical model in AstroPosition:
Deactivate all astrometric corrections to obtain better agreement in longitudes:
Compute the geocentric latitude of Paris from its geodetic latitude:
It now agrees with the latitude reported by AstroPosition:
GeoPositionXYZ[loc] is equivalent to AstroPosition[loc,"ITRS","Cartesian"]:
Deactivate all astrometric corrections to obtain full agreement:
GeoPositionENU[loc,origin] is equivalent to AstroPosition[loc,{"Horizon","Location"origin},"CartesianENU"]:
Deactivate all astrometric corrections to obtain full agreement:
Related Guides
History
Text
Wolfram Research (2022), AstroPosition, Wolfram Language function, https://reference.wolfram.com/language/ref/AstroPosition.html.
CMS
Wolfram Language. 2022. "AstroPosition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AstroPosition.html.
APA
Wolfram Language. (2022). AstroPosition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AstroPosition.html
BibTeX
@misc{reference.wolfram_2025_astroposition, author="Wolfram Research", title="{AstroPosition}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/AstroPosition.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_astroposition, organization={Wolfram Research}, title={AstroPosition}, year={2022}, url={https://reference.wolfram.com/language/ref/AstroPosition.html}, note=[Accessed: 03-March-2026]}