Greater

x>y

が より大きいと判定されるとTrueを返す．

x1>x2>x3

が狭義減少数列をなす場合，Trueを返す．

詳細

  • Greaterは，強不等式あるいは厳密な不等式としても知られている．
  • Greaterはその引数が実数である場合，TrueまたはFalseを返す．
  • Greaterは，引数が数でなければある簡約化を実行する．
  • 厳密な数において，Greaterは数値順序付けを行うために，数値近似を内部的に使う．この手続きは，大域変数$MaxExtraPrecisionの設定に影響を受けることがある．

例題

すべて開くすべて閉じる

例  (2)

数を比較する：

不等式を表す：

スコープ  (9)

数値不等式  (7)

不等式は実数についてのみ定義される：

有理数を比べる：

二進法で最高でも最後の8桁しか違わない近似数は等しいとみなされる：

厳密な数値表現と近似数を比較する：

2つの厳密な数式を比較する．不等式の証明には数値テストで十分なことがある：

この不等式の証明には記号的なメソッドが必要である：

Greaterで使われる数値メソッドと記号メソッドでは，この不等式が誤りであると証明するのには不十分である：

RootReduceを使って代数的数の符号を決定する：

Greaterが使う数値メソッドは，この不等式を証明するのに十分な精度ではない：

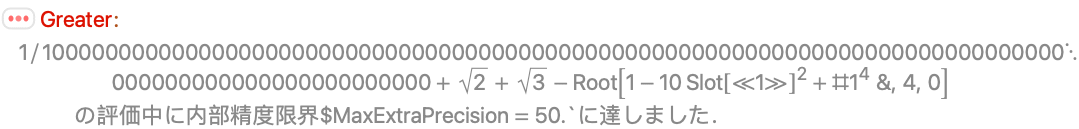
RootReduceは厳密なメソッドを使ってこの不等式を証明する：

$MaxExtraPrecisionの値を大きくすることによっても，この不等式が証明できるかもしれない：

記号不等式  (2)

x は実数ではないかもしれないので，記号不等式は未評価のまま残される：

Refineを使い，x が実数であると仮定して不等式を再評価する：

記号不等式：

Reduceを使って解集合の明示的な表示を求める：

FindInstanceを使って解の例を求める：

Minimizeを使って，不等式で定義された領域での最適化を行う：

Refineを使って不等式で定義された仮定の下で簡約する：

特性と関係  (12)

2引数のGreaterの否定はLessEqualである：

3引数のGreaterの否定は自動的には簡約されない：

LogicalExpandを使って，否定を2引数のLessEqualで表す：

これは，3引数のLessEqualとは等しくない：

Greaterが数式間の不等性が判断できない場合，不等式は未評価で返される：

FullSimplifyは厳密な記号変換で不等式が正しくないことを証明する：

Positive[x]は と等価である：

Reduceを使って不等式を解く：

FindInstanceを使って解の例を求める：

RegionPlotおよび RegionPlot3Dを使って不等式の解集合を可視化する：

不等式の仮定：

MinimizeおよびMaximizeを使って不等式で制約された最適化問題を解く：

NMinimizeおよびNMaximizeを使って制約条件付き最適化問題を数値的に解く：

不等式の解集合上で関数を積分する：

Median，Quantile，Quartilesを 番目の最大数に使う：

考えられる問題  (3)

機械精度の近似数についての不等式は微妙である：

厳密な不等性は余分な桁に依存している：

任意精度の近似数にはこの問題はない：

自動精度追跡機能のお陰で，Greaterは最初の10桁だけを見ればよいと分かっている：

この場合，機械数間の不等式は予想の結果を返す：

Greaterはこの場合の余分桁を無視する：

Wolfram Research (1988), Greater, Wolfram言語関数， https://reference.wolfram.com/language/ref/Greater.html （1996年に更新）.

テキスト

Wolfram Research (1988), Greater, Wolfram言語関数， https://reference.wolfram.com/language/ref/Greater.html （1996年に更新）.

CMS

Wolfram Language. 1988. "Greater." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Greater.html.

APA

Wolfram Language. (1988). Greater. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Greater.html

BibTeX

@misc{reference.wolfram_2024_greater, author="Wolfram Research", title="{Greater}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Greater.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_greater, organization={Wolfram Research}, title={Greater}, year={1996}, url={https://reference.wolfram.com/language/ref/Greater.html}, note=[Accessed: 21-November-2024 ]}