Quartiles

Quartiles[data]

gives the quantile estimates of the elements in data.

Quartiles[data,{{a,b},{c,d}}]

uses the quantile definition specified by parameters a, b, c, d.

Quartiles[dist]

gives the quantiles of the distribution dist.

Details

  • is equivalent to the median. »
  • is equivalent to the average of the medians of the and smallest elements in data if is odd, and the median of the smallest elements if is even.
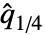  • is defined like , but with the largest rather than smallest elements.
  • For MatrixQ data, the quartile is computed for each column vector with Quartiles[{{x1,y1,…},{x2,y2,…},…}] equivalent to {Quartiles[{x1,x2,…}],Quartiles[{y1,y2,…}]}. »
  • For ArrayQ data, quartiles are equivalent to ArrayReduce[Quartiles,data,1]. »
  • Quartiles[data] is equivalent to Quantile[data,{1,2,3}/4,{{1/2,0},{0,1}}]. »
  • Quartiles[data,{{a,b},{c,d}}] is equivalent to Quantile[data,{1,2,3}/4,{{a,b},{c,d}}].
  • Common choices of parameters {{a,b},{c,d}} include:
  • {{0,0},{1,0}}inverse empirical CDF
    {{0,0},{0,1}}linear interpolation (California method)
    {{1/2,0},{0,0}}element numbered closest to p n
    {{1/2,0},{0,1}}linear interpolation (hydrologist method; default)
    {{0,1},{0,1}}mean‐based estimate (Weibull method)
    {{1,-1},{0,1}}mode‐based estimate
    {{1/3,1/3},{0,1}}median‐based estimate
    {{3/8,1/4},{0,1}}normal distribution estimate
  • The default choice of parameters is {{1/2,0},{0,1}}. »
  • The data can have the following additional forms and interpretations:
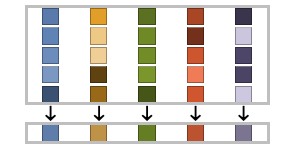
  • Associationthe values (the keys are ignored) »
    SparseArrayas an array, equivalent to Normal[data] »
    QuantityArrayquantities as an array »
    WeightedDatabased on the underlying EmpiricalDistribution »
    EventDatabased on the underlying SurvivalDistribution »
    TimeSeries, TemporalData, …vector or array of values (the time stamps ignored) »
    Image,Image3DRGB channel's values or grayscale intensity value »
    Audioamplitude values of all channels »
    DateObject, TimeObjectlist of dates or list of times »
  • Quartiles[dist] gives the list 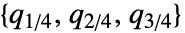corresponding to Quantile[dist]. »
  • For a random process proc, the quartiles function can be computed for slice distribution at time t, SliceDistribution[proc,t], as Quartiles[SliceDistribution[proc,t]]. »

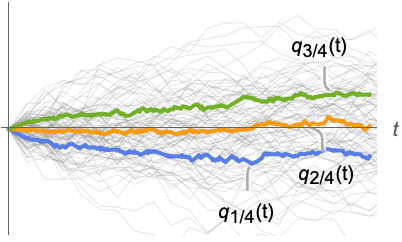
Examples

open allclose all

Basic Examples  (3)

Quartiles for a list of exact numbers:

Quartiles of a list of dates:

Quartiles of a parametric distribution:

Scope  (22)

Basic Uses  (8)

Exact input yields exact output:

Approximate input yields approximate output:

Compute results using other parametrizations:

Find the quartiles of WeightedData:

Find the quartiles of EventData:

Find the quartiles of TemporalData:

Find the quartiles of TimeSeries:

The quartiles depend only on the values:

Find the quartiles for data involving quantities:

Array Data  (5)

Quartiles for a matrix gives columnwise quartiles:

Quartiles for a tensor gives columnwise medians at the first level:

Works with large arrays:

When the input is an Association, Quartiles works on its values:

SparseArray data can be used just like dense arrays:

Find quartiles of a QuantityArray:

Image and Audio Data  (2)

Channelwise quartile values of an RGB image:

Quartile intensity values of a grayscale image:

Quartile amplitudes of all channels:

Date and Time  (4)

Compute quartiles of dates:

Compute the weighted quartiles of dates:

Compute the quartiles of dates given in different calendars:

The mean is given in one of the input calendars:

Compute the quartiles of times:

List of times with different time zone specifications:

Distributions and Processes  (3)

Find the quartiles for a parametric distribution:

Quartiles for a derived distribution:

Data distribution:

Quartile functions for a random process:

Applications  (4)

Quartiles divide a distribution in four equal probability sections:

Find a moving quartile envelope for a time series:

Data smoothed by moving median:

Moving envelope of first and third quartiles:

Find the quartiles for data representing the top oil-producing fields in 2001:

Compare with the minimum and maximum values for the data:

Plot the data with quartile lines:

Compute the quartiles for the heights of children in a class:

Properties & Relations  (6)

Quartiles are given by linearly interpolated Quantile values:

The default parameters for Quantile give a different result:

The second quartile of the data is the Median:

The quantile of 1/2 does not average the two middle elements for lists of even length:

InterquartileRange is the difference between the first and third quartiles:

QuartileDeviation is half the difference between the first and third quartiles:

QuartileSkewness is a skewness measure obtained from the quartiles:

BoxWhiskerChart shows the quartiles for data:

Possible Issues  (2)

Quartiles requires numeric values in data:

The symbolic closed form may exist for some distributions:

Quartiles of data computed via Quantile do not always agree with Quartiles:

Specify linear interpolation parameters in Quantile:

Wolfram Research (2007), Quartiles, Wolfram Language function, https://reference.wolfram.com/language/ref/Quartiles.html (updated 2024).

Text

Wolfram Research (2007), Quartiles, Wolfram Language function, https://reference.wolfram.com/language/ref/Quartiles.html (updated 2024).

CMS

Wolfram Language. 2007. "Quartiles." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Quartiles.html.

APA

Wolfram Language. (2007). Quartiles. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quartiles.html

BibTeX

@misc{reference.wolfram_2025_quartiles, author="Wolfram Research", title="{Quartiles}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Quartiles.html}", note=[Accessed: 04-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_quartiles, organization={Wolfram Research}, title={Quartiles}, year={2024}, url={https://reference.wolfram.com/language/ref/Quartiles.html}, note=[Accessed: 04-May-2025 ]}