HankelH1

HankelH1[n,z]

gives the Hankel function of the first kind .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
is given by .
HankelH1[n,z] has a branch cut discontinuity in the complex z plane running from 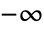to .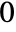
For certain special arguments, HankelH1 automatically evaluates to exact values.
HankelH1 can be evaluated to arbitrary numerical precision.
HankelH1 automatically threads over lists.
HankelH1 can be used with a CenteredInterval object. »

Examples

open allclose all

Basic Examples (5)

Evaluate numerically:

Plot the real and imaginary parts of the function:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Scope (33)

Numerical Evaluation (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number input:

Evaluate efficiently at high precision:

HankelH1 threads elementwise over lists and matrices:

HankelH1 can be used with a CenteredInterval object:

Specific Values (4)

Limiting value at infinity:

Evaluate HankelH1 symbolically for noninteger orders:

HankelH1 for symbolic n:

Find the first positive maximum for the real part of HankelH1[1/2,x]:

Visualize the result:

Visualization (4)

Plot the absolute values and phase of the HankelH1 function for various orders:

Plot the real and imaginary parts of the HankelH1 function for various orders:

Plot the real part of :

Plot the imaginary part of :

Plot the real part of :

Plot the imaginary part of :

Function Properties (7)

Complex domain for is the whole plane except :

It is not defined as a function from to :

HankelH1 is a complex linear combination of BesselJ and BesselY:

For integer and arbitrary fixed , $TemplateBox[{{-, n}, z}, HankelH1]=(-1)^n TemplateBox[{n, z}, HankelH1]$ :

is not an analytic function of :

HankelH1 is not injective over complexes:

Use FindInstance to find inputs that demonstrate it is not injective:

has both singularities and discontinuities along the negative real axis:

TraditionalForm formatting:

Differentiation (3)

First derivative with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z when n=2:

Formula for the derivative with respect to z:

Integration (3)

Compute the indefinite integral using Integrate:

Definite integral:

More integrals:

Series Expansions (6)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

General term in the series expansion using SeriesCoefficient:

Asymptotic approximation of HankelH1:

Find series expansion for an arbitrary symbolic direction :

Taylor expansion at a generic point:

HankelH1 can be applied to a power series:

Applications (1)

There can be subtleties with asymptotic approximation when the function to be approximated approaches zero infinitely many times in every neighborhood of the approximation point. As an example, consider the asymptotic expansion of near :

Consider the approximation of the never-zero Hankel function :

This approximation is asymptotic:

So is the approximation of the Hankel function of the second kind, :

As , its approximation can be understood as nearly asymptotic, being the sum
of two such approximations:

Properties & Relations (2)

Use FunctionExpand to convert to Bessel functions:

Integrate expressions with HankelH1:

Possible Issues (1)

HankelH1 does not automatically evaluate symbolically for half-integer arguments:

Use FunctionExpand to obtain an expanded form:

Top

HankelH1

Details

Examples

Basic Examples (5)