HankelH2[n,z]
gives the Hankel function of the second kind ![]() .
.




HankelH2
HankelH2[n,z]
gives the Hankel function of the second kind ![]() .
.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
![TemplateBox[{n, z}, HankelH2] TemplateBox[{n, z}, HankelH2]](Files/HankelH2.en/2.png) is given by
is given by ![TemplateBox[{n, z}, BesselJ]-iTemplateBox[{n, z}, BesselY] TemplateBox[{n, z}, BesselJ]-iTemplateBox[{n, z}, BesselY]](Files/HankelH2.en/3.png) .
. - HankelH2[n,z] has a branch cut discontinuity in the complex z plane running from
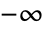 to
to 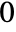 .
. - For certain special arguments, HankelH2 automatically evaluates to exact values.
- HankelH2 can be evaluated to arbitrary numerical precision.
- HankelH2 automatically threads over lists.
- HankelH2 can be used with a CenteredInterval object. »
Examples
open all close allBasic Examples (5)
Plot the real and imaginary parts of the function:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (33)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
HankelH2 can be used with a CenteredInterval object:
Compute the elementwise values of an array:
Or compute the matrix HankelH2 function using MatrixFunction:
Specific Values (4)
Visualization (4)
Function Properties (7)
Complex domain for ![]() is the whole plane except
is the whole plane except ![]() :
:
It is not defined as a function from ![]() to
to ![]() :
:
HankelH2 is a linear combination of BesselJ and BesselY:
For integer ![]() and arbitrary fixed
and arbitrary fixed ![]() ,
, ![]() :
:
![]() is not an analytic function of
is not an analytic function of ![]() :
:
HankelH2 is not injective over complexes:
Use FindInstance to find inputs that demonstrate it is not injective:
![]() has both singularities and discontinuities along the negative real axis:
has both singularities and discontinuities along the negative real axis:
TraditionalForm formatting:
Differentiation (3)
Integration (3)
Series Expansions (6)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Asymptotic approximation of HankelH2:
Find series expansion for an arbitrary symbolic direction ![]() :
:
Taylor expansion at a generic point:
HankelH2 can be applied to a power series:
Applications (1)
There can be subtleties with asymptotic approximation when the function to be approximated approaches zero infinitely many times in every neighborhood of the approximation point. As an example, consider the asymptotic expansion of ![]() near
near ![]() :
:
Consider the approximation of the never-zero Hankel function ![]() :
:
This approximation is asymptotic:
So is the approximation of the Hankel function of the second kind, ![]() :
:
As ![]() , its approximation can be understood as nearly asymptotic, being the sum
, its approximation can be understood as nearly asymptotic, being the sum
of two such approximations:
Properties & Relations (2)
Possible Issues (1)
HankelH2 does not automatically evaluate symbolically for half-integer arguments:
Use FunctionExpand to obtain expanded form:
See Also
Tech Notes
Related Guides
Related Links
History
Text
Wolfram Research (2007), HankelH2, Wolfram Language function, https://reference.wolfram.com/language/ref/HankelH2.html.
CMS
Wolfram Language. 2007. "HankelH2." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HankelH2.html.
APA
Wolfram Language. (2007). HankelH2. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HankelH2.html
BibTeX
@misc{reference.wolfram_2025_hankelh2, author="Wolfram Research", title="{HankelH2}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/HankelH2.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_hankelh2, organization={Wolfram Research}, title={HankelH2}, year={2007}, url={https://reference.wolfram.com/language/ref/HankelH2.html}, note=[Accessed: 10-March-2026]}